Latent Factor Models
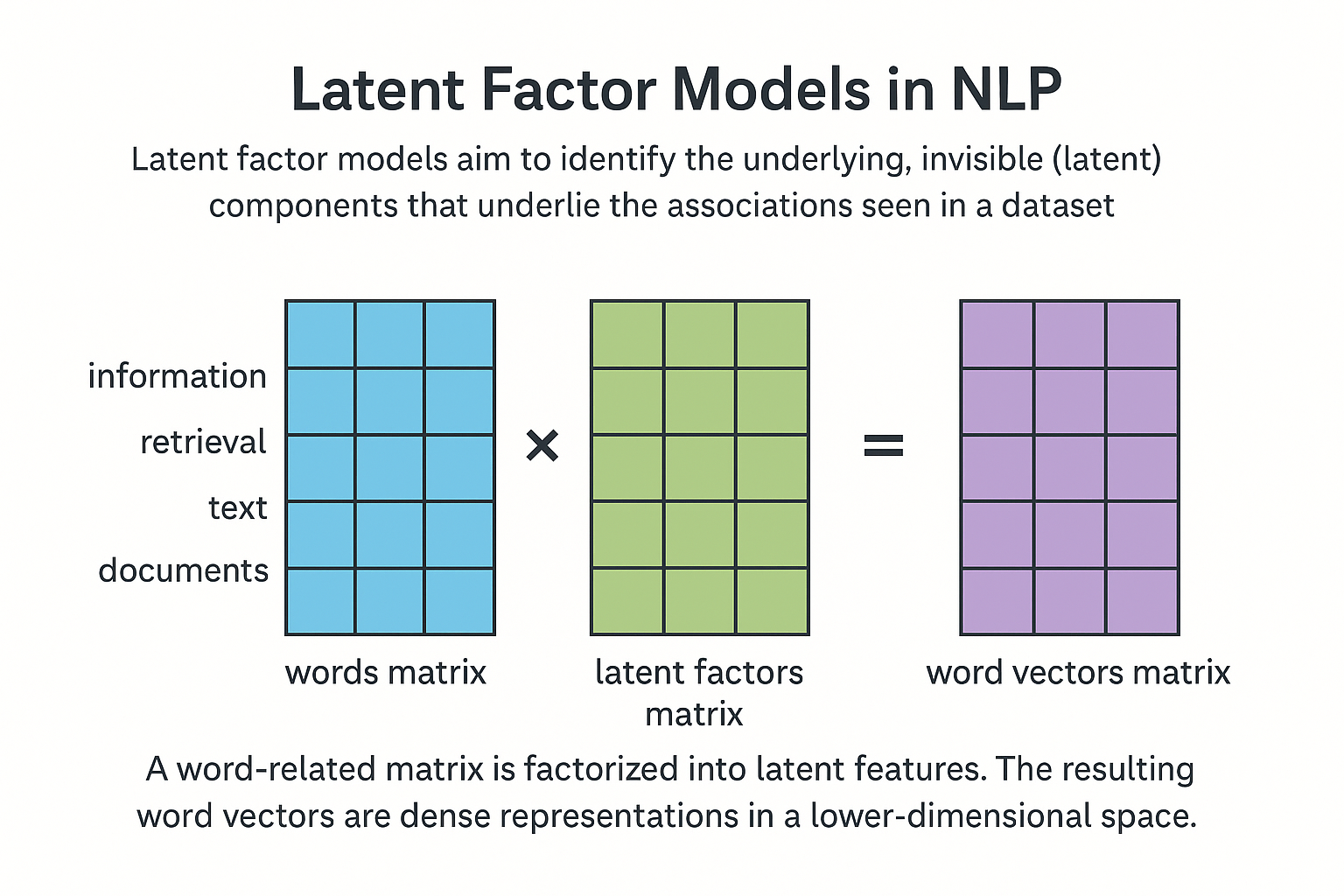
A family of methods known as latent factor models aims to identify the underlying, invisible (latent) components that underlie the associations seen in a dataset. Representing words, documents, or word-context interactions in a lower-dimensional vector space the dimensions of which are known as “latent factors” is a common practice in natural language processing.
Main Concept
These models are based on the core premise that fewer underlying latent components or ideas may account for observed high-dimensional data, such as co-occurrence counts between many words and many documents or between words and their context words. The models seek to minimise the complexity of the data and capture significant semantic linkages by identifying these elements.
Traditional Approaches (Explicit Matrix Factorization)
- Explicit matrix factorization encompasses a number of early and significant NLP techniques, especially for learning word or document representations. In order to identify lower-dimensional representations, these techniques entail building a sizable matrix that depicts some kind of link between things (for example, words and documents or words and situations) and then breaking this matrix down.
- One well-known example is Latent Semantic Analysis (LSA), also known as Latent Semantic Indexing (LSI). LSA starts by creating a matrix, such a document-by-word matrix, whose entries show the frequency of words in documents or their weighted frequency (TF-IDF, for example).
- After that, this matrix is broken down into several component matrices using a mathematical process called Singular Value Decomposition (SVD). A lower-rank matrix approximates the original matrix by retaining just the top k singular values and their accompanying vectors. With k being the selected number of latent components (dimensions), this procedure projects the initial high-dimensional data onto a k-dimensional subspace.
- In this latent space, the vector representations for words and documents are the resultant lower-dimensional vectors (derived from the SVD components). These vectors’ dimensions match the latent elements that the decomposition revealed.
- Non-negative matrix factorization (NMF) and Probabilistic Latent Semantic Indexing (PLSI) are two further explicit matrix factorization techniques. PLSI is connected to Latent Dirichlet Allocation (LDA), which is frequently used for topic modelling and may be considered in this light.
Neural Network Connections (Implicit Matrix Factorization)
- It has been demonstrated that contemporary neural network designs, in particular autoencoders and certain word embedding models, may implicitly learn representations that are mathematically comparable to or analogous to those generated by matrix factorisation. There is no explicit construction or decomposition of the matrix in a separate stage.
- Neural networks taught to recreate their input are called autoencoders; this is usually accomplished via a bottleneck layer that has fewer units than the input layer. A condensed, lower-dimensional representation of the input is learnt by this bottleneck layer. Numerous matrix factorization types, such as SVD, NMF, PLSA, and logistic matrix factorization, may be simulated using autoencoders. They may carry out various forms of factorization with variations in the neural architecture, such as the selection of the output layer’s activation function (softmax for categorical data, sigmoid for binary data).
- As we previously discussed, a popular neural method for learning word embeddings, the Skip-gram model with Negative Sampling (SGNS) variant of Word2vec, implicitly factorizes a matrix associated with the word-context Pointwise Mutual Information (PMI) or Positive Pointwise Mutual Information (PPMI) matrix. Indicating that the word vectors acquired by SGNS efficiently function as the latent components derived from a matrix factorization of (a modified form of) the word-context co-occurrence matrix, this relationship was emphasised. Word2vec models may be thought of as nonlinear matrix factorization variants of autoencoders.
Learning
- SVD is utilised directly in explicit matrix factorisation techniques such as LSA.
- The Expectation-Maximization (EM) algorithm is a popular method for estimating parameters for probabilistic latent variable models that incorporate latent states, like Latent Dirichlet Allocation or HMMs. A broad framework for learning with latent or missing data is called EM.
- Gradient descent or its variations, such as stochastic gradient descent, are commonly used in neural network-based techniques (such as autoencoders or Word2vec) to train the latent factor representations (the embedding vectors and associated weights).
In conclusion, the goal of latent factor models in natural language processing is to represent linguistic input in a condensed, significant subspace that is specified by hidden factors. This can be done implicitly by training neural networks (like autoencoders or Word2vec) whose architecture and training goal cause them to learn representations that correspond to these underlying latent factors, or explicitly by factoring large co-occurrence matrices using methods like SVD (as in LSA). Dense vector representations that capture different semantic features and the connections between words and documents are produced by these models.
