A strong signal processing method with many uses, sparse decomposition is especially useful for feature extraction and denoising.
What is sparse decomposition?
A signal or data sample can be represented as a linear combination of a few basis elements (also known as atoms) from an overcomplete dictionary using the sparse decomposition technique, which is used in machine learning and signal processing. Finding the sparsest representation that is, one in which the majority of the coefficients are zero or very close to zero—is the main idea. This helps with anomaly identification, feature extraction, compression, and denoising. L1 regularization is frequently used to solve optimization problems in sparse decomposition techniques (e.g., Lasso). Applications include image processing, audio separation, and compressed sensing, where only limited measurements are available but the underlying signal is sparse.
A concept in digital signal processing (DSP) called “sparse decomposition” entails expressing a signal as a linear combination of a few fundamental operations or “atoms” from an extensive lexicon. The main concept is to approximate the original signal by determining the best linear combination of these dictionary entries. The goal of this procedure is to eliminate crowded noise signals and retrieve pure distinctive peaks.
Sparse decomposition effectively obtains spectrum characteristics in Raman spectroscopy by adaptively merging and removing different disturbances from the original signal.
Also Read About What is Deconvolutional network? and its Architecture, Mechanism
How sparse decomposition works?
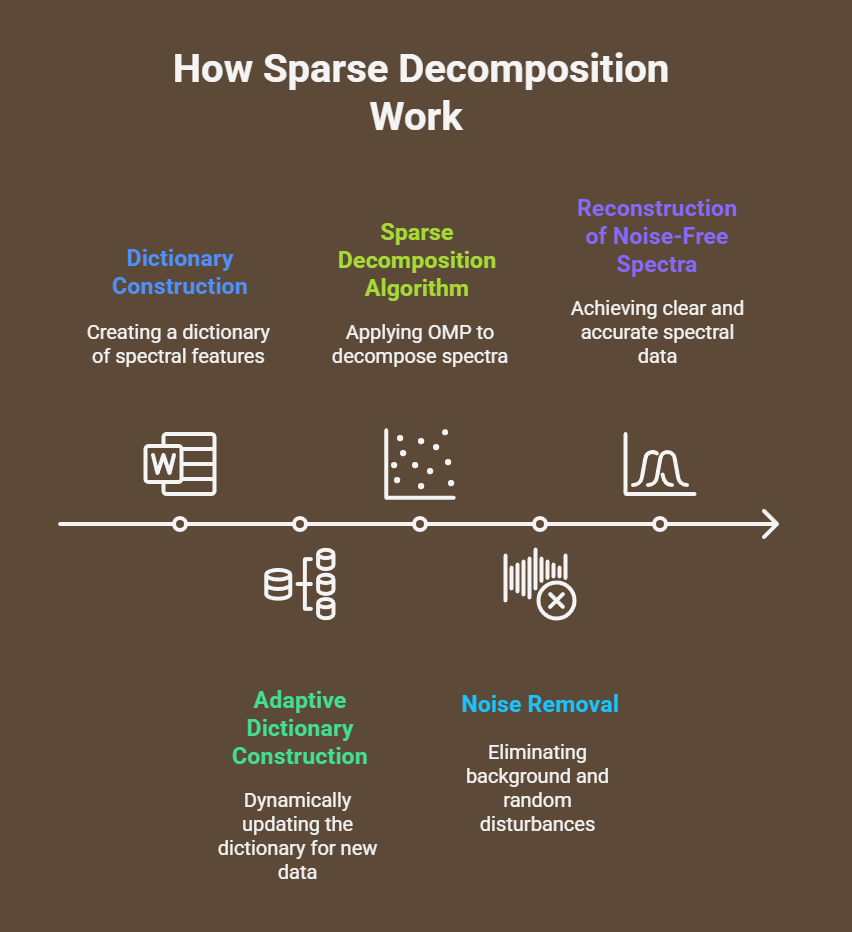
The basic steps in sparse decomposition are as follows architecture and process:
Dictionary Construction: A thorough dictionary made up of fundamental functions or peaks of spectral features is created. The structure of the signal being approximated should be closely matched by this dictionary. Using chemometric feature extraction techniques, this can be accomplished from the input spectra for Raman spectra, improving the dictionary’s alignment with the original data.
Adaptive and Dynamic Dictionary Construction: A dynamic dictionary construction technique is presented in order to overcome the drawbacks of fixed dictionaries, particularly for novel or unknown compounds and changeable instruments. This approach combines the capability to dynamically create a dictionary in the event that no match is found in an offline dictionary database that contains spectra of different chemicals from multiple instruments for universality. This ensures versatility by enabling the dictionary database to be expanded.
Sparse Decomposition Algorithm: A collection of column vectors inside the generated dictionary that provides the best linear combination to represent the original signal is found using a greedy or adaptive tracking technique. Raman spectra are sparsely decomposed onto the built dictionaries using the orthogonal matching pursuit (OMP) algorithm. This procedure successfully removes a variety of background and random disturbances, enabling the reconstruction of noise-free spectra.
History
The sources show that sparse decomposition is a fundamental and recurring problem in many fields and has been widely used in image and signal processing, even though they do not give a thorough historical timeline of the technique. A relatively recent advancement covered in the texts offered is its use in the pre-processing of Raman spectra.
Also Read About What are Conditional Variational Autoencoders CVAE
Benefits
Particularly for Raman spectra, the Adaptive Sparse Decomposition Denoising (ASDD) approach has the following important benefits:
Improved Accuracy and Robustness
It makes denoising Raman spectra more accurate and robust.
Effective Noise Elimination
Shot noise, dark current noise, emission noise, and material background fluorescence are just a few of the random and background sounds that it successfully removes.
Characteristic Peak Preservation
ASDD may overcome the drawback of existing algorithms’ low denoising performance and maintain more pertinent Raman characteristic peaks. Additionally, it improves peak forms to satisfy specified requirements and resolves the issue of typical peak shape distortion.
Enhanced Analytical Accuracy
ASDD improves the precision of drug classification and concentration prediction by offering clearer spectra.
Universality and Adaptability
By combining offline and dynamic dictionary generation, ASDD can quickly adjust to new substances with little extra information. Its universality is increased by its ability to adjust to spectra obtained by the majority of sensors.
Less Data Needed
It eliminates the need to build sizable datasets for machine learning algorithms by requiring very little data for dictionary training.
Better Performance
Empirical findings verify that ASDD performs better than current algorithms for analyzing Raman spectra, especially pesticide spectra. The drawbacks of existing denoising algorithms are addressed, including characteristic peak types that deviate from normal peak forms, frequent retention of clutter and random noise, and restricted baseline effects.
Disadvantages and Limitations
Although effective, sparse decomposition techniques have limits, especially in their older implementations:
- Vocabulary Dependence: Having a comprehensive vocabulary of Raman characteristic peaks is a crucial prerequisite.
- Fixed Dictionary Issues: Conventional sparse decomposition techniques frequently use fixed dictionaries, which yield less-than-ideal denoising results since they are not well-suited for fitting real Raman signals.
- Real vs. generated Data: Earlier techniques for sparse representation of Raman spectra relied on dictionaries based on generated Gaussian signals, which may not match the precise conditions of real Raman spectra. By doing this, characteristic peaks that are not inherent to the particular chemical may not be eliminated.
- Calculation Accuracy: Compared to more recent techniques like OMP employed in ASDD, some matching pursuit algorithms may have somewhat worse calculation accuracy even when they have desired denoising benefits.
Features
The following are important aspects of sparse decomposition, particularly as it is used in ASDD:
- Adaptive Linear Combination: The capacity to describe the signal and remove noise by adaptively combining dictionary entries.
- Using a dictionary of fundamental operations or spectral characteristics is known as dictionary-based representation.
- Feature extraction: This technique is intended to efficiently extract intrinsic features from intricate signals.
- Multi-noise Elimination: Able to remove multiple types of noise at once, such as background fluorescence noise and random noise (shot noise, dark current, emission noise).
- Peak Shape Enhancement: The capacity to enhance the distinctive peaks’ forms.
Also Read About What is an Extreme Learning Machines? and Limitations of ELMs
Types (and Applications)
A general idea used in many fields, sparse decomposition frequently has specialized applications:
Raman Spectral Denoising (ASDD)
An inventive adaptive technique designed especially for Raman spectra, Raman Spectral Denoising (ASDD) aims to improve quality and get past obstacles caused by noise and impurity peaks. This technique can be used to domains that use Raman spectra, such as food analysis, life sciences, and customs surveillance. It has demonstrated strong performance in predicting concentration and classifying substances.
Low-Rank Matrix Decomposition
This technique is used to identify distinct low-dimensional matrix decompositions and is useful in fields such as numerical analysis, machine learning, signal processing, and optimisation and control.
Graph Neural Networks (GNN)
By approximating node representations using a chosen subset of nodes, sparse decomposition approaches are being developed to lower the inference cost of GNNs. In applications like node classification and spatiotemporal forecasting, this seeks to attain linear complexity in terms of average node degree and number of layers, surpassing alternative approaches for inference speedup.
Two-Dimensional Signals
Two-dimensional signals are likewise subject to sparse decomposition.
General Image and Signal Processing
This fundamental idea is widely used in these domains.
Challenges
ASDD and other advanced sparse decomposition techniques seek to address the following main issues:
- Complex Noise Nature: Handling the existence of impurity peaks in signals such as Raman spectra and the complicated nature of noise.
- A disadvantage of conventional smoothing filters was their inability to maintain signal integrity, which ensures excellent accuracy while fitting different signal types without distorting characteristic peaks or incurring overall information loss.
- Over-fitting/Under-fitting: Preventing problems that can arise with conventional curve-fitting baseline correction techniques, such as over-fitting or under-fitting.
- Algorithm Performance Independence: This reduces the need for large, precise datasets to train, which is a drawback of several denoising algorithms based on neural networks.
- Dictionary Universality: Creating dictionaries that are not fixed or simulated but may successfully fit real signals and adjust to a variety of substances and equipment.
Also Read About What is an Echo State Networks? and Advantages of ESNs
In conclusion, sparse decomposition specifically the ASDD method represents a major breakthrough in signal preprocessing by offering a reliable, precise, and flexible method for feature preservation and noise reduction across a range of complicated data types.
