What is Merkle Proof
Originating from a data structure called a Merkle tree, which is mostly utilized for effectively confirming the integrity of data and transactions, Merkle proofs are a crucial part of blockchain technology. They are essential to the safe and scalable operation of decentralized networks.
What is a Merkle Tree and Merkle Root?
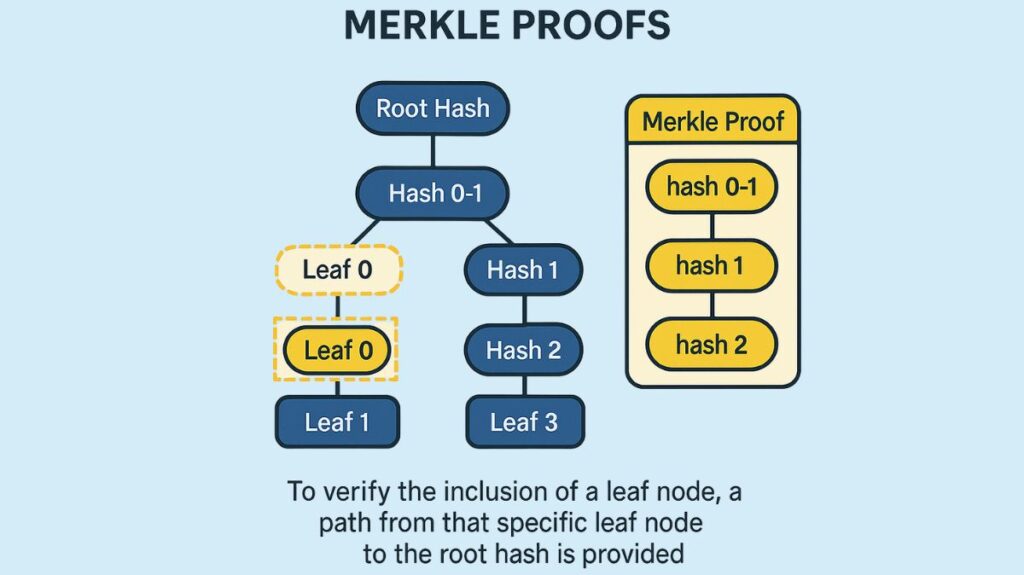
A tree-like data structure based on hashing algorithms is called a Merkle tree. Usually, it is shown with the individual data items at the bottom and inverted.
Leaves: The hashes of distinct data points, like transactions within a block, are represented by the leaves at the base of the tree. In Bitcoin, for example, the initial leaf nodes are created by applying a double SHA-256 hash function to the hashes of each individual transaction. Every leaf stands for a distinct, independently verifiable fact.
Parent Nodes: Each leaf node’s parent node is created by concatenating the hash of each pair of leaf nodes. Rehashing concatenated child nodes is a recursive procedure that keeps going up the tree. To guarantee that every node has a hashing partner, the hash from the most recent transaction is simply copied or replicated to create a pair if there are an odd number of transactions at any level.
Merkle Root: Until a single, distinct hash value referred to as the Merkle root is reached at the very top of the tree, this procedure is repeated. The Merkle root functions as a fingerprint or cryptographic synopsis of all the underlying information. The Merkle root is extremely vulnerable to data manipulation since even a slight change to one leaf node will produce an entirely different Merkle root.
Functionality and Purpose in Blockchain
One important component kept in the header of a block is the Merkle root. It provides a succinct cryptographic digest and functions as a digital fingerprint of every transaction in that block.
Important goals include:
Data Integrity Verification: A different hash at that level will unavoidably result from changing even a single bit of the data or hash within the Merkle tree in a single transaction. This hash will then spread higher, eventually leading to a different Merkle root. As a result, the system can swiftly identify any corruption or manipulation in the block’s transaction list without having to look at each transaction separately.
Efficient Transaction Verification: Instead of downloading and reviewing each transaction separately, full nodes in the network can confirm that they have the exact same list of transactions as other nodes by comparing their Merkle roots. This greatly reduces the amount of data that lightweight clients (SPV clients) must process because they just require the Merkle root from the block header.
Storage Efficiency: Because Merkle trees just need to store the data hashes which are fixed-length digests instead of the entire huge dataset, they are naturally storage economical. Additionally, this optimizes bandwidth utilization by making the “proofs” themselves much smaller and faster to send over the network.
How Merkle Proofs Work
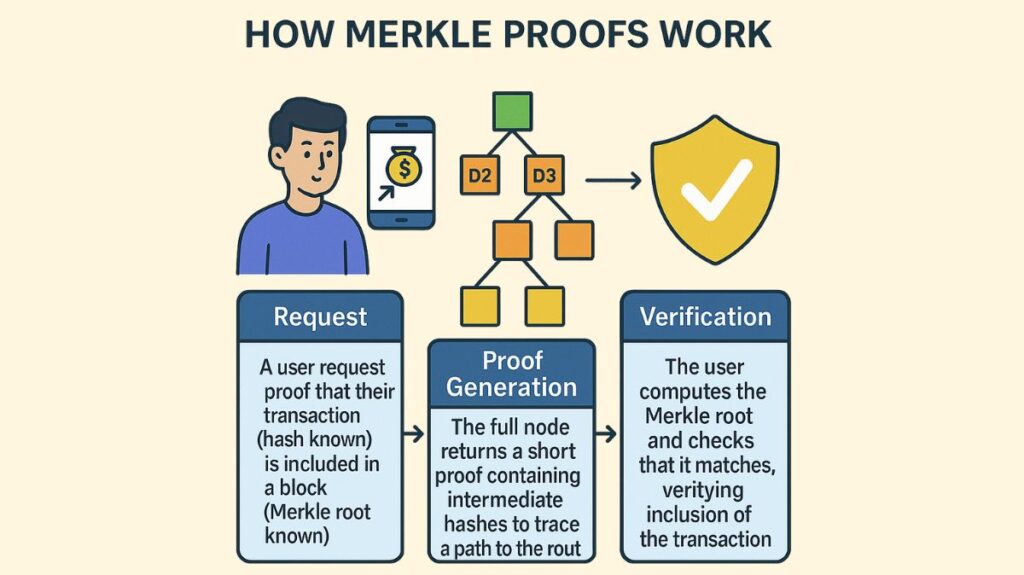
Without downloading or disclosing the contents of the full block, a user can cryptographically demonstrate that a particular transaction or piece of data is part of it using a Merkle proof. For decentralized networks to be efficient and private, this is essential.
Request: A complete node is asked by a user (or “light client” with little processing and storage capacity) to confirm that their record (transaction D2, for example) is in fact part of the Merkle tree of a specific block. The hash of the transaction and the Merkle root of the entire block are already known to the user.
Proof Generation: The entire block is not sent by the full node. Rather, it returns a small collection of intermediate hashes from the Merkle tree (also known as the “authentication path” or “Merkle branch”). This contains just enough information to rebuild the path to the root, including the hash of the transaction in question and the hashes of its sibling nodes at each level up the tree.
Verification: The hashes can then be separately calculated upward by the user. To arrive to a single computed Merkle root, they first combine the hash of their known transaction with the first sibling hash that is given, then hash the result with the next sibling hash, and so on. The inclusion of the transaction in that block is cryptographically confirmed as valid if this computed root precisely matches the Merkle root kept in the authentic block header (which the light client usually possesses).
This procedure guarantees that:
- The transaction offers strong cryptographic certainty because it is in fact a component of the block that produced that particular Merkle root.
- Since it can produce genuine intermediary hashes that lead to the known root, the system supplying the proof is legitimate.
- For light clients, this greatly improves network efficiency while protecting anonymity by revealing very little about the full tree or other transactions.
Merkle Proof Applications
Merkle trees are essential components that form the foundation of the security and effectiveness of all significant blockchains, including Ethereum and Bitcoin.
Bitcoin: In Bitcoin, transactions are combined into a single Merkle tree, and the block header contains the Merkle root that results. The integrity of every transaction within the block is then guaranteed by hashing this root and other block header data to create the block’s unique identifier, or block hash.
Ethereum: Merkle-Patricia trees, a more sophisticated variant, are used in the Ethereum blockchain. Three such trees are contained in each block header: one for transactions, one for transaction receipts (transaction results), and one for the status information of the entire network. The blockchain’s state can be updated in a very effective and verifiable manner with its intricate structure.
SPV Clients: Partial or lightweight nodes, sometimes referred to as Simple Payment Verification (SPV) clients, merely save a copy of the block headers of the longest valid blockchain a negligible quantity of information. By examining the Merkle branch that connects a particular transaction to the Merkle root in the block header where it was accepted, they mostly rely on Merkle proofs to confirm payments. This makes blockchain accessible on devices with limited capacity (such as mobile phones) and enables effective transaction verification without requiring the download and storage of the complete blockchain.
Efficiency, integrity, and security are the main advantages. The hash of a transaction within a block would change if it were modified, which would modify the Merkle root and set off a series of changes up the Merkle tree. This strengthens the immutability of the blockchain by making any tampering immediately identifiable and invalidating that block as well as all blocks that are constructed upon it.
Merkle Proof Features
Tree-like Data Structure: A Merkle tree, a hierarchical, tree-like data structure constructed using hashing methods and usually shown upside down, is the source of Merkle proofs.
Leaf Nodes: The cryptographic hashes of discrete data points, such transactions within a blockchain block, make up the “leaf” nodes at the base of the tree.
Parent Nodes: Recursively hashing the concatenation of the hashes of their child nodes creates intermediate “parent” nodes that move upward.
Merkle Root: The Merkle root, a single, distinct hash value at the top, is the result of the procedure. This root serves as a digital fingerprint or condensed cryptographic summary of all the information in the tree.
Proof Generation: A complete node provides a tiny collection of intermediary hashes (a “Merkle branch”) that make up a Merkle proof. Just enough information is included in this branch to cryptographically link a particular transaction hash to the Merkle root as a whole.
Verification Process: Users, particularly light clients, can recalculate the upward path by using these sibling hashes that are provided in conjunction with the hash of their transaction. The inclusion of the transaction is confirmed if their calculated root corresponds to the known Merkle root in the block header.
Cryptographic Security: Any change to a single piece of data or hash within the tree will affect the Merkle root, making manipulation instantly obvious because to the reliance on cryptographic hashing.
Merkle Proof Advantages
Data Integrity Verification: Data integrity can be quickly and reliably verified with Merkle proofs. The resulting Merkle root will change if even a single byte of data or hash within the tree is changed, immediately indicating tampering without requiring a full dataset analysis.
Efficient Transaction Verification: They make it possible to verify a transaction’s inclusion in a block very quickly. Instead than downloading the full big block of transactions, lightweight clients (SPV clients) can verify that a transaction is a part of a block by downloading just the block header, which contains the Merkle root, and a short Merkle proof.
Storage Efficiency: Because Merkle trees only require a single, fixed-length Merkle root to represent potentially enormous volumes of data, they are storage efficient. Additionally, the proofs themselves are compact, which lowers the amount of storage needed for verification.
Bandwidth Optimization: Merkle proofs’ small size optimizes bandwidth use for users and nodes by requiring less data to be sent across the network for verification.
Decentralized Trust: In decentralized settings, they provide trustless verification. The cryptographic hash algorithms and the known block header are the only things a user has to trust, not the entire node supplying the proof.
Fundamental to Blockchains: A key component of all major blockchains, including Ethereum and Bitcoin, Merkle trees support their security paradigm and allow for scalable light client operation.
Merkle Proof Disadvantages
Requires a Full Node for Proof Generation: Light clients cannot create Merkle proofs, but they can effectively verify them. A party needs to be able to reconstruct the Merkle tree, which usually calls for a complete node, and have access to the entire block’s transaction data in order to provide a Merkle proof for a particular transaction.
Complexity in Implementation (for certain types): More sophisticated variations, such as Ethereum’s Merkle-Patricia trees, are considerably more difficult to implement and maintain than basic Merkle trees, which might present possible error areas for developers.
Proof Size Can Grow with Tree Depth: A Merkle proof’s size scales logarithmically with the number of transactions, despite being typically tiny. The proof might grow somewhat, but still be far less than the complete data, for very huge blocks with (theoretically) millions of transactions.
