Proof of Non-Membership (PoNM)
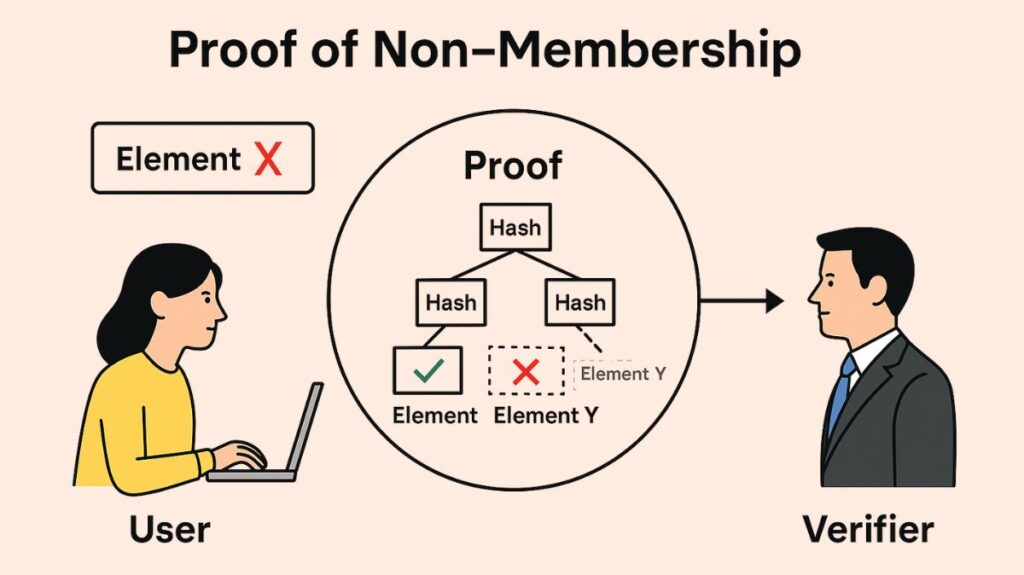
It is possible for one person, called the prover, to persuade another, called the verifier, that a certain element does not belong to a given set by using a cryptographic primitive called a Proof of Non-Membership (PoNM). Importantly, this is accomplished without disclosing the complete set or any more details other than the element’s unmistakable non-membership. This feature, which permits verifiable claims on the absence of data, is essential for improving privacy and security in a variety of digital systems.
Why is PoNM Important?
Even though PoNM seems abstract, it has a lot of real-world uses, especially in secure systems and privacy-preserving technology. Without disclosing private information that may be included in the set, it tackles situations when you need to effectively and safely demonstrate something’s absence. This talent is essential in a world where data is becoming more and more important.
Some important use cases are:
Blockchain & Cryptocurrencies: In blockchains that priorities privacy, such as Zcash or Monero, PoNM can be used to verify that a certain transaction is not part of a particular block, that an address has not yet claimed an airdrop, or that a coin or private note has not yet been spent. This is essential in some privacy models to avoid double-spending without disclosing transaction history.
Databases: Verifying that a key or record is missing from a database without disclosing all of the information contained inside. Providing proof that one is not on a watch list (such as a sanctions list or a no-fly list) without disclosing one’s identify to the list holder or the list’s secret entries is an example of how this may work.
Authentication Systems & Revocation Lists: Demonstrating that neither a user’s credentials nor a digital certificate are on a blacklist of unauthorized users or a Certificate Revocation List (CRL). Without downloading or disclosing potentially large and sensitive revocation lists, this enables effective trust formation and access rights verification.
Compliance: Proving that a certain person is not on a watch list for financial crimes or that a transaction does not include a sanctioned business, all without disclosing the full private sanctions list or all transaction information. This fills the void between privacy and legal obligations.
Spam Filtering: Demonstrating that an email address is not on a list of senders that have been banned or known to be spammers, enabling email providers to effectively filter unsolicited communications while protecting the anonymity of their spam lists.
Decentralized Identity (DID): To improve the security and privacy of digital identity management, PoNM may be used in DID systems to verify that an identity has not been revoked or to demonstrate that a certain credential does not exist.
PoNM essentially enables quick and easy absence verification without jeopardizing the security, privacy, or accuracy of the sensitive data that lies beneath.
How Does PoNM Work?
It is sometimes more difficult to explicitly demonstrate an absence than a presence, which is the main obstacle in showing non-membership. If an element is in a set, it may be shown directly; if not, an indirect cryptographic method that depends on the intrinsic structure of the set is required. The cryptographic data structures used by the majority of PoNM techniques implicitly encode the set and enable verifiable calculations to validate the exclusion of a member.
The following are typical methods:
Merkle Trees (and variations like Sparse Merkle Trees):
- Data structures that resemble trees, known as Merkle Trees, have internal nodes that represent the hash of their child nodes and leaf nodes that reflect the hash of a data piece. Although they are mostly employed for effective membership proofs (demonstrating that an element is a part of a set), they may also be modified for non-membership.
- When proving non-membership, particularly with a sorted Merkle tree, the prover shows the cryptographic pathways to the two items that, if the missing element were in the sorted set, would come right before and after it. For example, if “grape” is not in a tree with “apple,” “banana,” and “cherry,” the pathways (and values) to “banana” and “cherry” would be part of the evidence. The verifier determines that there is nothing else that might be between these two items by confirming that they are members and that they are successive (adjacent) in the sorted set.
- An version known as Sparse Merkle Trees deals with circumstances in which certain tree slots are vacant. By proving that a placeholder value (such as a particular hash for “null” or “empty”) is present at the element’s location and that the element’s proper location is empty, non-membership is established.
- Advantages: Computationally efficient for verification, commonly utilized in blockchains, and somewhat easy to comprehend and use for sorted collections.
- Disadvantages: Enables efficient non-membership proofs by requiring the underlying set to be sorted, yet the proof size can still be logarithmic with respect to the set size, meaning it increases with bigger sets.
Cryptographic Accumulators:
- A cryptographic primitive known as an accumulator is capable of representing a vast number of components with a single, compact, fixed-size value (the “accumulator value”).
- Accumulators that efficiently handle both membership and non-membership proofs include RSA accumulators.
- When it comes to non-membership, it frequently uses the principles of complex number theory to demonstrate that the element cannot be written in a form that would suggest it is a part of the cumulative set. The proof may include a “witness” that mathematically proves non-membership when paired with the element and the accumulator value.
- Advantages: Extremely efficient for membership proofs, much shorter and more effective for non-membership proofs than Merkle Trees for extremely big sets, and very compact accumulator value and proofs (often constant size, independent of set size).
- Disadvantages: Some structures may need a trusted setup step (where initial parameters are produced safely and subsequently discarded) or rely on strong cryptographic assumptions, and thus are more mathematically complicated to comprehend and use. Additionally, compared to membership proofs, non-membership proof creation may need more computing power from the prover.
Zero-Knowledge Proofs (ZKPs):
- A proof of non-membership may be constructed with the help of general-purpose ZKPs (such as Zk-SNARKs or Zk-STARKs), which are strong and adaptable tools.
- To verify for non-membership, the prover builds a cryptographic circuit that encodes the reasoning (e.g., “Is ‘x’ not equal to any element in set ‘S’?” or “Is ‘x’ not present at any index ‘i’ in array ‘A’?”). The prover then, without disclosing ‘x’ or the set ‘S,’ makes a ZKP that they know fits this requirement. The verifier only verifies that the ZKP is genuine.
- Advantages: Extremely adaptable and provides the best privacy guarantees (zero-knowledge), as no information about the element or the set is disclosed other than the fact that it is not a member. is capable of managing intricate non-membership requirements.
- Disadvantages: Proofs are computationally costly and time-consuming to produce, particularly for big collections. Correct and efficient implementation of these is likewise quite difficult, and some (like Zk-SNARKs) could need a trusted setup.
Characteristics of a Good PoNM Scheme
The following crucial characteristics are usually included in a strong PoNM system to guarantee its dependability and usefulness:
Soundness: This is an essential security feature. In the event that the element is, in fact, present in the set, it guarantees that a malevolent prover cannot produce a legitimate evidence of non-membership. A plan would be open to misleading claims if it were not sound.
Completeness: Because of this characteristic, even if the element actually does not exist in the set, an honest prover may always produce a legitimate evidence of non-membership. It is impossible to show lawful non-membership in a scheme that is incomplete.
Zero-Knowledge/Privacy: This property is very desired yet optional. The evidence should protect the privacy and secrecy of the underlying data by disclosing nothing about the element or the contents of the set (other than the fact that it is not a member).
Efficiency: The prover’s and verifier’s processes should be computationally reasonable and not need excessive amounts of time, CPU, or memory, particularly as the size of the set increases.
Proof Size: Regardless of the size of the collection, the proof itself need to be modest in order to facilitate storage and transmission. Its size should ideally be logarithmic or constant.
Example: Proving Non-Membership in a Sorted Merkle Tree
Let’s look at a straightforward example where wish to demonstrate that the number “7” is not included in the sorted set S{2,5,8,12,15}, which is represented by a Merkle Tree.
Construct the Merkle Tree: The leaves of the tree are formed by hashing the sorted set items. Parent nodes are created by combining and re-hashing each pair of leaf hashes, and this process is repeated upward until a single Merkle Root is produced.
Leaves: H(2),H(5),H(8),H(12),H(15). (Assume H() is the hash function).
First Level Parent Nodes:: H(H(2)∣∣H(5)),H(H(8)∣∣H(12)),H(H(15)∣∣H(15)) (if using duplication for odd numbers).
Root: Represents the whole set, the last hash at the top of the tree.
Prove that “7” is NOT in Set S:
Prover’s Action: Five and eight are the two items in the sorted set S that the prover determines “surround” seven. The verifier is then given by the prover:
- The Merkle route (the series of sibling hashes required to calculate H(5) up to the root) and the value 5 that correspond to it.
- The Merkle route (the series of sibling hashes required to calculate H(8) up to the root) and the value 8 that correspond to it.
- The fact that 5 and 8 are nearby (consecutive) items in the initial sorted set is confirmed by an implicit or explicit assertion or proof element.
Verifier’s Action: 5 and its Merkle path are sent to the verifier, along with 8 and its Merkle path.
- Initially, the verifier compares both Merkle pathways to the established, reliable Merkle Root of the set S. This attests to the fact that 5 and 8 are both valid members of set S.
- Next, the verifier confirms that 5 and 8 are indeed sequential in the set’s sorted order (neither the tree structure nor the evidence presented include any additional elements between them).
- Lastly, the verifier determines that 7 is not in the set S since 5 and 8 are numerically and cryptographically sequential, verified members, and the number 7 falls between them.
Challenges and Future Directions of PoNM
Even with its increasing usefulness, Proof of Non-Membership still has problems that scholars are working to solve:
Efficiency: Proof generation and verification can still be computationally demanding for both the prover and the verifier, particularly when dealing with very large sets or complicated non-membership criteria (like ZKPs). Optimising algorithms is still a top priority.
Scalability: When dealing with huge datasets in real-world applications (such as worldwide blacklists or enormous registries), it is imperative that these approaches scale efficiently as the size of the underlying collection increases.
Dynamic Sets: The problem is to handle additions and deletions from the set efficiently without needing a “rebuilding” or a full recalculation of the entire underlying data structure (such as the accumulator or Merkle tree). Merkle trees are rather good at handling additions and deletions at the leaf level, but accumulators may find updates more complicated.
Universality: Minimizing the need for highly specialized solutions for every use case by creating more efficient and universal constructs that function in a variety of environments and cryptographic setups.
Ease of Use & Integration: Lowering the barrier to entry and simplifying the integration of these intricate cryptographic primitives into programs without the need for extensive cryptographic knowledge.
Since digital interactions are becoming more complicated and require better privacy and verified data absence, proof of non-membership is still an important and constantly developing subject in current cryptography.
| Feature | Description |
|---|---|
| Definition | Proof that an element is not part of a set |
| Purpose | To show non-membership without revealing full set |
| Tools used | Merkle Trees, Sparse Merkle Trees, RSA Accumulators |
| Proof size | Small, even for big sets |
| Use cases | Blockchain, databases, airdrops, revocation lists |
