Hopfield Network explained
A Hopfield Network is a type of recurrent content-addressable memory in computer science, proposed by John Hopfield in 1982. It is designed to store and retrieve patterns and is often used for auto-association and optimization tasks.
Here’s a detailed explanation of Hopfield Networks:
What is a Hopfield Network?
One type of recurrent artificial neural network (ANN) is a Hopfield Network. Except for itself, every neuron in its single layer is connected to every other neuron. Usually, these connections are symmetric and bidirectional. As a content-addressable memory, the network is resilient to faulty or incomplete data since it can reconstruct entire patterns from noisy or partial inputs.
Hopfield network architecture

- The network is made up of numerous neurons, which are simple, equivalent parts.
- Each neuron functions as an “on or off” neuron and can be in one of two states: Vi = 0 (“not firing”) or Vi = 1 (“firing at maximum rate”).
- Tij, the strength of the connection between neurons, is defined by Tij = 0 for neurons that are not connected. Strong back-coupling, or recurrent connections, is a crucial component of Hopfield Networks that sets them apart from previous models like Perceptron’s and accounts for their intriguing emergent characteristics.
- Additionally, every neuron has a preset threshold Ui, which is normally set to 0 in the model.
- Because the system uses asynchronous parallel processing, neurons independently and randomly change their states over time.
History
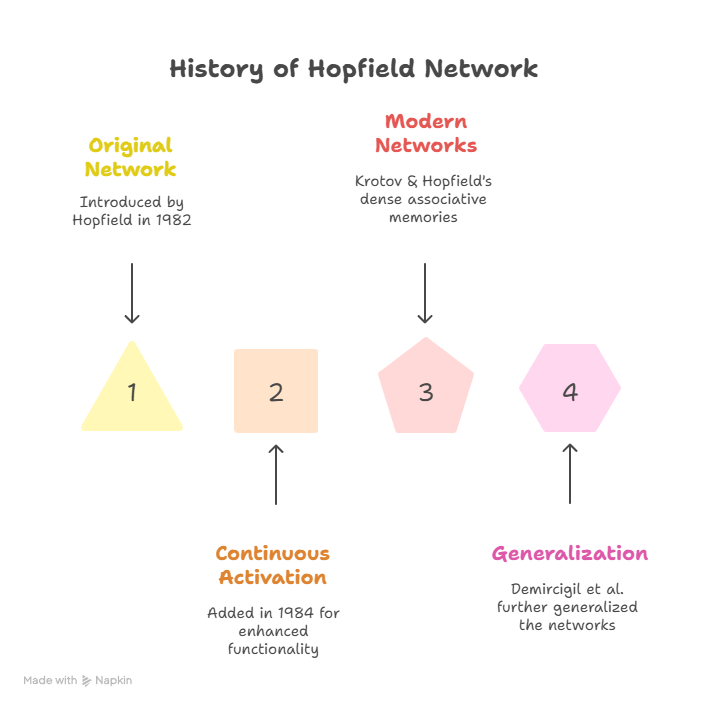
History of the Hopfield Network
How it Works
In order for a Hopfield Network to function, its state must undergo transitions until it stabilizes.
- State Initialization: An input pattern sets certain processing nodes to an “active” or “firing” state (output ‘1’) and others to an “inactive” state (output ‘0’), initializing the state of the network.
- Update Rule: The weighted sum of inputs from other neurons is used to update neurons (or units).
- If the entire weighted input for a binary neuron (0/1 or +1/-1) surpasses a threshold, which is usually zero, the neuron fires (output 1 or +1); if not, it is inhibited (output 0 or 1).
- Until the network’s state stabilizes, that is, stops changing, this procedure is repeated.
- Energy Function (Lyapunov Function): A Hopfield Network is characterized by an energy function, which is a scalar value associated with each state of the network. This energy function monotonically decreases or stays the same with each update.
- The dynamics of the network are designed to converge to a local minimum of this energy function in every case. The stored patterns match these local minima.
- With weights enforcing constraints that affect outputs and push the system towards low-energy states, the network functions as a constraint fulfilment network.
- Update Methods: There are two methods for performing updates:
- Asynchronous: Either randomly or according to a preset order, only one unit is updated at a time. If weights are symmetric, this approach ensures convergence to a stable state.
- Synchronous: A central clock is necessary since all units are updated at the same time. This may converge to a limit cycle of length two or a stable state.
Advantages of Hopfield Network
Associative Memory: Hopfield Networks excel at content-addressable memory, allowing the recovery of complete patterns from noisy or partial inputs.
One-Shot Memorization/Learning: The Sparse Quantized Hopfield Network (SQHN) is one model that can train quickly and conduct one-shot memorization.
Optimization Problems: They can be used to solve combinatorial optimization problems, where the desired solution corresponds to the minimization of the network’s Lyapunov function.
Robustness: The pattern may be identified even when the input is disrupted, demonstrating their resilience to faults.
Biological Plausibility (in some variants): Newer models, such as SQHN, have characteristics that are compatible with biological brains, such as sparse coding, neuron proliferation (neurogenesis), and local learning principles. For example, the function and observable characteristics of the SQHN memory node, such as synaptic flexibility and fast neuron development, are similar to those of the hippocampus.
Disadvantages/Challenges
Spurious Patterns: One major disadvantage is the potential for convergence to “spurious patterns” that are local energy minima but are not part of the initially taught patterns. These could be linear combinations of stored patterns or negations.
Limited Storage Capacity: It is challenging to store a high number of vectors without making many mistakes because of the limited memory storage capacity of classical Hopfield networks, which scales linearly with the number of input features. For dimension d, the error-free retrieval capacity is about d / (2*log(d)), or 0.14d for patterns with minor errors.
Correlation Sensitivity: If stored patterns are highly connected, retrieval may be subpar.
Computational Cost: With several neuron updates needed for each iteration, Predictive Coding Networks (PCNs), which are somewhat comparable to Hopfield Networks, can be computationally costly for online learning.
Complexity with High-Dimensional Data: The network may find it difficult to manage complex and high-dimensional data.
Key Features
Recurrent Neural Network: Neurons feed back into each other, creating a dynamic system.
Content-Addressable Memory: Partial or noisy input cues can be used to retrieve patterns.
Binary/Bipolar Nodes: Generally, neurons exist in discrete states, such as 0/1 or +1/-1. There are other nodes with continuous values.
Symmetric Weights (no self-connections): Neurons do not connect to themselves (W_ii = 0), and the strength of the connection between neuron I and neuron J is the same as that between neuron I and neuron J (W_ij = W_ji).
Energy Function (Lyapunov Function): A scalar function whose value decreases or remains constant with network updates, ensuring convergence to a stable state.
Local Learning Rules: Only information that is local to the synapses can influence synaptic modifications. One well-known example is the Hebbian learning rule.
Types
- Discrete Hopfield Network: Uses binary (0/1) or bipolar (+1/-1) inputs and outputs to operate in discrete time steps.
- Continuous Hopfield Network: Treats time as a continuous variable, with neurons having continuous, graded outputs (e.g., between 0 and 1). The energy of the network decreases continuously.
- Modern Hopfield Networks (Dense Associative Memories): A generalization that achieves much larger store capacity (super-linear or even exponential in the number of feature neurons) by utilizing new energy functions (such as exponential or higher-order polynomial interaction functions).
- These contemporary networks’ update rule is comparable to transformer networks’ attention mechanism, particularly when they use a log-sum-exponential Lagrangian function.
- They are able to function with states and patterns of continuous values.
- Modern Hopfield networks can be further layered to create Hierarchical Associative Memory Networks, which allow for symmetric feedforward and feedback weights and varying neuron counts, activation functions, and time scales per layer.
Hopfield Network Applications
Associative Memory: The primary application, including auto-association (associating a pattern with itself) and hetero-association (associating two different patterns). SQHN, for instance, outperforms state-of-the-art networks in these tasks.
Optimization Problems: Resolving intricate combinatorial optimization issues, including worker assignment, linear programming, and the traveling salesman problem.
Image processing: For image denoising, super-resolution photos, and noise reduction.
Episodic Memory: SQHN models have demonstrated exceptional efficacy in episodic recognition tests, even going beyond capacity to differentiate between fresh and old data points. Experiments on animal and human memory served as inspiration for this.
Online-Continual Learning: In online, continuous learning scenarios, SQHN models perform well, learning effectively with noisy inputs and exhibiting less catastrophic forgetting. For embedded systems like robots and sensing devices, this is essential.
Pattern Recognition and Correction: This technique is used to identify patterns, fix errors, and extract entire patterns from incomplete or distorted data.
Deep Learning Architectures: The Hopfield layers (Hopfield, HopfieldPooling, and HopfieldLayer) of contemporary Hopfield Networks can be incorporated into deep learning architectures as plug-in substitutes or for novel uses such as attention mechanisms, multiple instance learning, and set-based learning. DeepRC is an example of classifying immunological repertoires.
