What Is Single Layer Perceptron Neural network Architecture

What is Single Layer Perceptron?

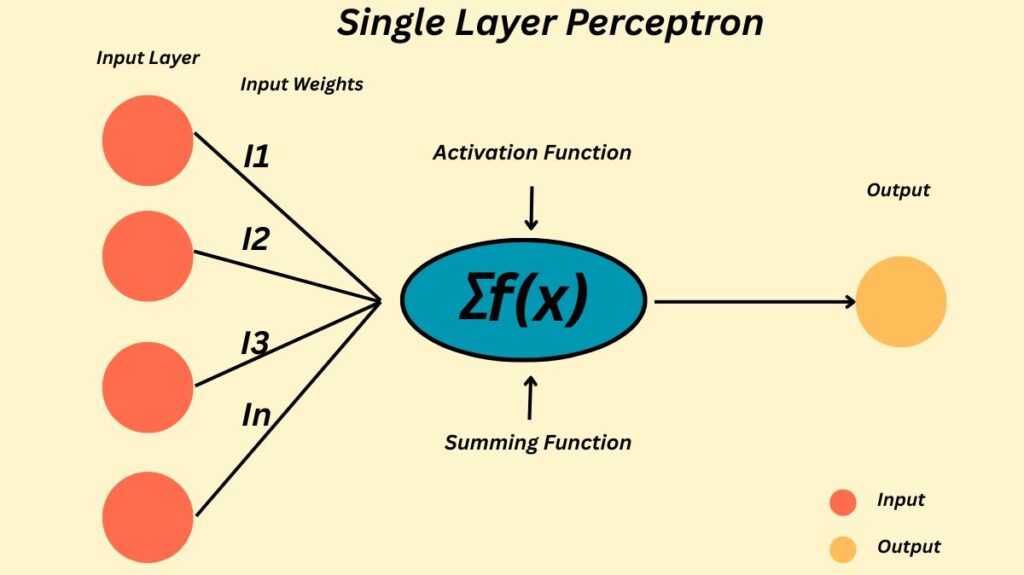
One of the most basic kinds of feedforward networks is the Single Layer Perceptron (SLP), a basic kind of artificial neural network. The input nodes are directly coupled to a single layer of artificial neurons, known as perceptrons. An SLP does not have any hidden layers.

For data classification, the Single Layer Perceptron (SLP) is an early and basic model of an Artificial Neural Networks. Frank Rosenblatt developed it in the 1960s and initially offered it as a neuronal model. The perceptron model is still a popular neural network model in domains including computer vision, pattern recognition, and machine learning.

Understanding Artificial Neural Networks (ANNs)

One must first understand Artificial Neural Networks (ANNs) in order to grasp a single layer perceptron. The operation of biological neural circuits serves as the model for the mechanisms of artificial neural networks (ANNs), which are information processing systems. An artificial neural network is made up of numerous interconnected processing units. The number of layers, the level of nodes between inputs and outputs, the number of neurones per layer, and the pattern of connections between nodes all determine a neural network’s design. The two main architecture types of ANNs are Single Layer Perceptrons and Multi-Layer Perceptrons.

Architecture and Computation of a Single Layer Perceptron

One layer of links connects the input and output nodes of a single layer perceptron, which is why it is referred to as a “single-layer” network. Input and output nodes are the two layers of nodes that are usually present.

This is the process by which it is calculated:

Input Nodes: Multi-dimensional input, such as x = (I1, I2,…, In), can be expressed as a vector and is received by these nodes (or units).

Weighted Sum: A node (or several nodes) on the following layer are usually fully coupled to input nodes. A weighted sum of all inputs is calculated by a node in the next layer. In order to do this, each input value must be multiplied by a matching weight vector element. For instance, the summed input would be I1w1 + I2w2 + I3w3, where wi is the weight corresponding to input Ii, if input x = (I1, I2, I3). Positive or negative weights are both possible.

Bias: A BIAS, or base value, is frequently used as the first input value to normalise the dataset.

Activation Function/Threshold: The input of an activation function is the value that is shown in the output. As an alternative, a threshold (t) value is used.

• The perceptron “fires” when the sum of the inputs is more than or equal to the threshold (summed input >= t), and the output (y) is 1.
• The output (y) is 0 and it does not fire if the total input is less than the threshold (summed input < t).
• The result would be rounded to zero, for instance, if the threshold was 0.5 and the sum was 0.43.

Training a Single Layer Perceptron

Based on training data, the perceptron learns by modifying its thresholds and weights.

Initialization: Random values are used to initialise the weights at the start of training.

Error Calculation: The error is determined by subtracting the intended output from the actual output for every element in the training set.

Weight Adjustment: After that, the weights are modified using the computed error. This procedure is carried out repeatedly until either a maximum number of iterations (epochs) is reached or the error on the entire training set falls below a predetermined threshold.

Gradient Descent: Gradient descent is the algorithm used to update weights.

Perceptron Learning Rule:

• Weights (wi) for active input lines (where Ii=1) are increased and the threshold is lowered if the correct output (O) is 1 and the actual output (y) is 0 (indicating that the output is insufficiently large). This is meant to boost the output.
• Likewise, the threshold is raised and weights (wi) for active input lines (Ii=1) are decreased if y=1 and O=0 (indicating that the output is excessively large). The goal of this is to reduce the output.
• No adjustments are performed to the weights or thresholds if the actual output is the same as the correct output (y=O).
• For weights, this adjustment formula is wi := wi + C * (O - y) * Ii, and for the threshold, it is t := t - C * (O - y), where C is a positive learning rate.

Convergence: There is a convergence proof that shows the perceptron algorithm will converge and place a decision surface (a hyperplane) between two linearly separable classes if the training examples are from those classes.

Examples and Capabilities

In essence, a perceptron distinguishes between inputs that trigger it to fire and those that don’t. This is done by drawing a line in 2D input space or a hyperplane in n-dimensional input space that is described by the formula w1I1 +… + wnIn = t. One category applies to points on one side of this line or hyperplane, while the other category applies to points on the other side. Whether or not data is linearly separable determines a perceptron’s classification capacity.

OR Gate:

A well-known illustration of linear separability is the OR gate dataset:

• x1 x2 y
• 1 1 1
• 1 0 1
• 0 1 1
• 0 0 0 A straight line can be drawn to divide the outputs of this dataset since it is linearly separable. Weights that could be used for an OR perceptron include threshold t=1, w1=1, and w2=1. The line I1 + I2 = 0.5 is drawn to separate the points (0,1), (1,0), and (1,1) from (0,0) in the following alternate example: w1=1, w2=1, and t=0.5.

AND Gate: Another illustration of what a single-layer perceptron can do. Weights such as w1=1, w2=1, and threshold t=2 are possible examples.

Image Classification (Logistic Regression): For picture classification tasks, a single layer perceptron can be employed, as demonstrated by its representation using Logistic Regression. Implementing logistic regression for the MNIST dataset (handwritten digit recognition) is demonstrated by the TensorFlow code that is supplied. This entails:

• Factors such as batch size, training epochs, and learning rate.
• Establishing placeholders for the goal output (y) and input (x).
• Configuring the model’s biases (b) and weights (W).
• Softmax activation function construction for the model.
• Minimizing error with the Gradient Descent Optimizer and cross entropy.
• The model is trained by fitting training data, calculating average loss, and looping through batches and epochs.
• Lastly, the accuracy of the model is tested.

Limitations: The XOR Problem

The incapacity of the single-layer perceptron to tackle problems that are not linearly separable is a major drawback. The most well-known instance of this is the exclusive OR (XOR) problem:

• input output
• 0,0 0
• 0,1 1
• 1,0 1
• 1,1 0 Because it is impossible to create a single straight line to divide the points (0,0) and (1,1) from (0,1) and (1,0), a single-layer perceptron cannot implement XOR. The creation and advancement of multi-layer networks was prompted by this fundamental constraint.