Stochastic Gradient Variational Bayes
Stochastic Gradient Variational Bayes (SGVB) is a potent technique for approximation Bayesian inference that is mostly applied to neural networks. It is especially helpful when working with models that involve latent variables, such as Variational Autoencoders (VAEs) or Bayesian Neural Networks (BNNs).
What is Stochastic Gradient Variational Bayes (SGVB)?
A technique for approximate Bayesian inference is called SGVB. Its main idea is to use observed data to estimate the posterior distribution of latent variables or model parameters (such as neural network weights), particularly when it is impossible to compute the true posterior distribution directly. SGVB offers a computationally effective framework that scales to the requirements of deep learning architectures and big datasets while achieving the advantages of Bayesian modelling, such as uncertainty quantification.
History
The historical chronology of SGVB’s evolution is not covered in full by the cited. The underlying backdrop for techniques like Variational Stochastic Gradient Descent (VSGD), which make use of stochastic variational inference, is the recent and growing interest in developing gradient-based optimizers within a probabilistic framework.
Fundamental Issue and Resolution of Stochastic Gradient Variational Bayes
Analytical solutions of expectations with regard to the estimated posterior are frequently needed for the traditional variational Bayesian (VB) technique, which can be unfeasible in most situations.
In order to resolve this, SGVB demonstrates how a simple, differentiable, and unbiased estimator of the lower bound may be obtained by reparameterizing the variational lower bound. Standard stochastic gradient techniques can then be used to directly optimise this estimation. Accordingly, it eliminates the requirement for costly iterative inference algorithms per datapoint, like Markov Chain Monte Carlo (MCMC).
How it Works
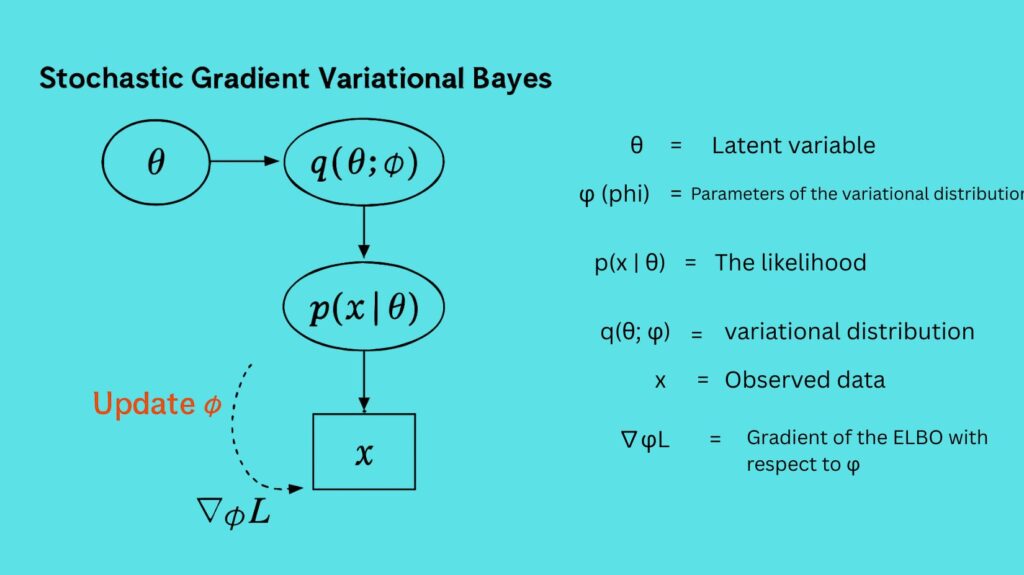
By fusing two key ideas, variational inference and stochastic gradients, SGVB tackles the intractable nature of posterior distributions.
Variational Inference
- SGVB uses a more straightforward, tractable distribution called the variational distribution to approximate the genuine posterior distribution rather than computing it.
- Usually, a neural network is used to parameterize this variational distribution.
- Reducing the Kullback-Leibler (KL) divergence between the true posterior and the variational distribution is the goal.
- Mathematically, maximizing the Evidence Lower Bound (ELBO) is comparable to minimizing this KL divergence.
Stochastic Gradients
- Expectations that are intractable in and of themselves are frequently involved in maximizing the ELBO.
- Stochastic gradient descent (SGD) is used by SGVB to optimize the variational distribution’s parameters.
- This optimization, which is scalable to huge datasets, is accomplished by taking unbiased, noisy estimates of the ELBO’s gradients, usually using mini-batches of data.
Key Techniques for Gradient Estimation
- Reparameterization Trick: This is a crucial innovation for continuous latent variables. It allows gradients to be passed through the sampling process, making the objective differentiable concerning the variational parameters. This technique enables the gradient computation to be amenable to standard backpropagation.
- Log-Derivative Trick (REINFORCE): This is an alternative method that can be used when the reparameterization trick is not applicable. However, it often suffers from higher variance in gradient estimates.
Architecture
Stochastic Gradient Variational Bayes is a technique for approximation Bayesian inference and learning within pre-existing neural network topologies rather than a design in and of itself.
- The variational distribution is parameterized using neural networks.
- SGVB is used in Bayesian Neural Networks (BNNs) to estimate a distribution over the weights of the network.
- SGVB is essential to learning the parameters of the encoder, which maps data to a latent space, and the decoder, which reconstructs data from that latent space, in Variational Autoencoders (VAEs).
Advantages (Benefits)
Stochastic Gradient Variational Bayes offers several significant advantages, particularly in the realm of deep learning:
- Scalability: By using stochastic optimization, it makes approximation Bayesian inference possible in large-scale models such as deep neural networks.
- Uncertainty Quantification: SGVB offers a method for calculating the degree of prediction uncertainty in BNNs. For applications that require safety and sound decision-making, this is important.
- Generative Modelling: Strong generative models such as VAEs are supported by SGVB. It enables the creation of new samples and the learning of rich data representations.
- Computational Efficiency: At the deep learning architecture scale, it offers a computationally efficient framework for Bayesian inference.
Disadvantages
The overall drawbacks of Stochastic Gradient Variational Bayes are not specifically listed in the information provided. However, it should be mentioned that, in contrast to the reparameterization trick, the Log-Derivative Trick, an alternate technique for gradient estimation within SGVB, frequently has more variance in gradient estimations.
Features
Key features of SGVB include:
- Approximate Bayesian inference is being performed.
- optimization by the use of stochastic gradient descent.
- Using the log-derivative approach for effective gradient estimating or the reparameterization trick (for continuous latent variables).
- Tackling issues where it is impossible to determine the true posterior distribution.
- The variational distribution is parameterized using neural networks.
- Allowing for scalable learning and inference in latent variable models.
Types
Rather than describing various “types” of SGVB, they provide SGVB as a single approach or framework. The difference is frequently seen in the application domain (e.g., BNNs vs. VAEs) or the particular gradient estimation method employed (e.g., reparameterization trick vs. log-derivative trick).
Challenges
The “challenges” of SGVB itself are not specifically listed. Rather, they emphasize that SGVB is intended to tackle the difficulties that arise in Bayesian inference due to intractable expectations and posterior distributions. Higher variance is a hurdle for the Log-Derivative Trick, although this is unique to that technique and not a generic problem for SGVB in general.
Applications
Stochastic Gradient Variational Bayes has a wide range of applications, especially in deep learning:
- Bayesian Neural Networks (BNNs): Used to infer a distribution over the network’s weights, enabling the quantification of uncertainty in predictions. This is crucial for applications requiring high reliability, such as safety-critical systems.
- Variational Autoencoders (VAEs): SGVB is fundamental to VAEs, which are generative models that learn latent representations of data. It facilitates efficient approximate inference and learning of both the latent variable distribution and the data likelihood, allowing for the generation of new samples.
- Other Latent Variable Models: Scalable inference and learning are made possible by the extension of SGVB to a number of other probabilistic models involving latent variables.
- Deep learning-based Automatic Speech Recognition (ASR): SGVB has been applied in this domain.
- As an Optimizer (Variational Stochastic Gradient Descent – VSGD): A technique such as VSGD uses stochastic variational inference (SVI), which is closely connected to the concepts of SGVB, to construct an effective update algorithm for deep neural networks by modelling gradient updates as probabilistic models. In image classification tasks, it has been demonstrated to perform better than other adaptive gradient-based optimizers such as Adam and SGD.
