Let us learn about Latent Dirichlet Allocation and How Does Latent Dirichlet Allocation Work.
Latent Dirichlet Allocation
Topic modelling is the main application of the Latent Dirichlet Allocation (LDA) approach in natural language processing. One of the first methods for identifying latent structure in text is this one.
Purpose: To find themes in a corpus, LDA is utilized. Large text datasets are subjected to unsupervised learning in order to extract sets of related terms from the text. It is said to be a “very useful tool” for identifying a document’s thematic organization.
Classification: It is regarded as an alternative matrix model that developed after the first research on techniques based on Singular Value Decomposition (SVD), such as Latent Semantic Analysis (LSA). As models that followed the original SVD work, it is referenced in the same context as Non-negative Matrix Factorization (NMF) and Probabilistic Latent Semantic Indexing (PLSI). As early topic models, PLSI and NMF are also covered; it is highlighted that they are equivalent.
Nature: One type of latent variable model is LDA. The term “Dirichlet” suggests that LDA is probabilistic, even though the sources don’t go into great mathematical depth about it exactly. Both the Dirichlet Compound Multinomial distribution used in probabilistic text segmentation and the Dirichlet distribution as a typical prior for multinomial and categorical parameters in EM clustering for latent variable models are examples of related concepts that are frequently relevant in models such as LDA.
How Does latent Dirichlet allocation work
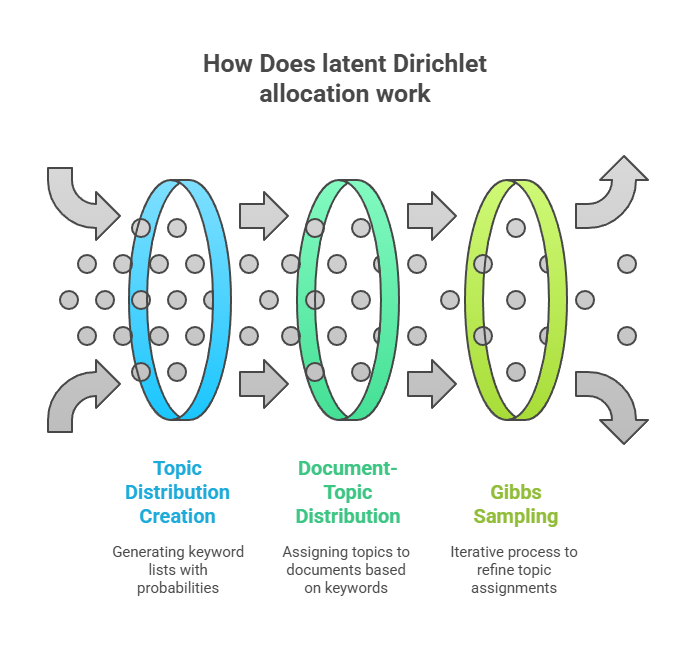
Latent Dirichlet allocation (LDA) treats documents as a “bag of words,” ignoring context and word order. Its main objective is to record, in a document-term matrix, the frequency and co-occurrence of terms in each document.
By presuming that words that appear together probably represent comparable themes, the LDA method uses this matrix to create topic distribution lists of keywords with probabilities. The word clusters in each document are then used to give document-topic distributions. Based on its wording, a paper may be classified as 95% Topic 1 (for instance, immigration) and 5% Topic 2 (for instance, astronomy).
Words with many meanings, such as “alien,” provide a problem. LDA uses Gibbs sampling to identify the subject of a word (and text). Two ratios are at the heart of the intricate mathematical formula:
- Topic ‘t”s likelihood in document ‘d’: By counting pertinent words, this determines how common subject “t” is in document “d.”
- Word ‘w”s likelihood of being associated with topic ‘t’: This establishes the frequency with which word ‘w’ occurs in subject ‘t’ across the corpus.
Remember that Gibbs sampling is iterative. Instead of being sampled once, words go through several iterations, continuously changing topic-word probabilities based on each other.
In conclusion, LDA is introduced as an unsupervised method for locating the “topics” that are buried inside a set of texts and determining the words that correspond to each subject. It is a member of the PLSI and NMF family of latent structure models that emerged subsequent to LSA. Latent variables are used in this probabilistic model.
It should be noted that the sources cited provide a high-level overview of LDA’s functions and its place in the field of NLP techniques, including topic modelling and matrix factorisation approaches. Neither the inference techniques employed in LDA nor the underlying probabilistic generating process are described in full.
