NLP With LSTM
Recurrent neural network (RNN) architectures include LSTMs. They were designed to tackle the vanishing gradient problem, which makes it hard for simple RNNs to learn and remember information across long sequences or time gaps.
Addressing Long-Term Dependencies
The information stored in the hidden states of basic RNNs is often local, even though they analyse sequences one element at a time and spread information through recurrent connections. In order to enable networks to use data that is far from the present point of processing, LSTMs were created. They are able to store knowledge and learn things with very large time gaps.
Core Mechanism
- Gates and Cell State: The addition of gating mechanisms and an explicit cell state (also known as a memory cell) is the primary innovation of LSTMs.
- Hidden State (ht): This is the state sent to the following time step as well as the output of the LSTM unit at the current time step. It is calculated by multiplying the result element-wise by the output gate output (ot) after the new cell state (ct) has been run through a tanh function (to scale values between -1 and 1).
- Equation: ht = ot ⊙ tanh(ct)
- (where tanh is the hyperbolic tangent function and ⊙ indicates element-wise multiplication). This concealed state frequently doubles as the LSTM unit’s output yt at time t.
- Through a mix of partial “forgetting” and “increment” processes, the cell state functions as a type of long-term memory, retaining information from previous states. Conceptually, it’s frequently thought of as a conveyor belt that transports data across the sequence.
- Equation: c̃t = tanh(Wc * [ht-1; xt] + bc)
- (where Wc is the cell state candidate’s weight matrix, bc is the cell state candidate bias, and tanh is the hyperbolic tangent function).
- Cell State Update (ct): Combining the prior cell state, the forget gate, the input gate, and the cell state candidate is where the magic happens. Information chosen by the forget gate is eliminated by multiplying the previous cell state (ct-1) element-wise by the forget gate output (ft). The additional information to be added is chosen by multiplying the cell state candidate (c̃t) element-wise by the input gate output (it). The new cell state (ct) is then created by adding these two outcomes.
- Equation: ct = ft ⊙ ct-1 + it ⊙ c̃t
- (where ⊙ stands for Hadamard product, or element-wise multiplication). Because it facilitates gradient flow through the network over extended time spans, this additive structure for updating the cell state is essential for solving the vanishing gradient problem. As a result, information storage is more persistent.
- Differentiable gating mechanisms regulate the information flow into and out of this cell state. The sigmoid activation function is commonly used to create these gates as smooth mathematical functions that produce values ranging from 0 to 1. These variables determine how much information should go through and may be thought of as soft, differentiable logic gates.
How NLP With LSTM Work
Types of Gates: To control the cell state, LSTMs use a variety of gate types, including:
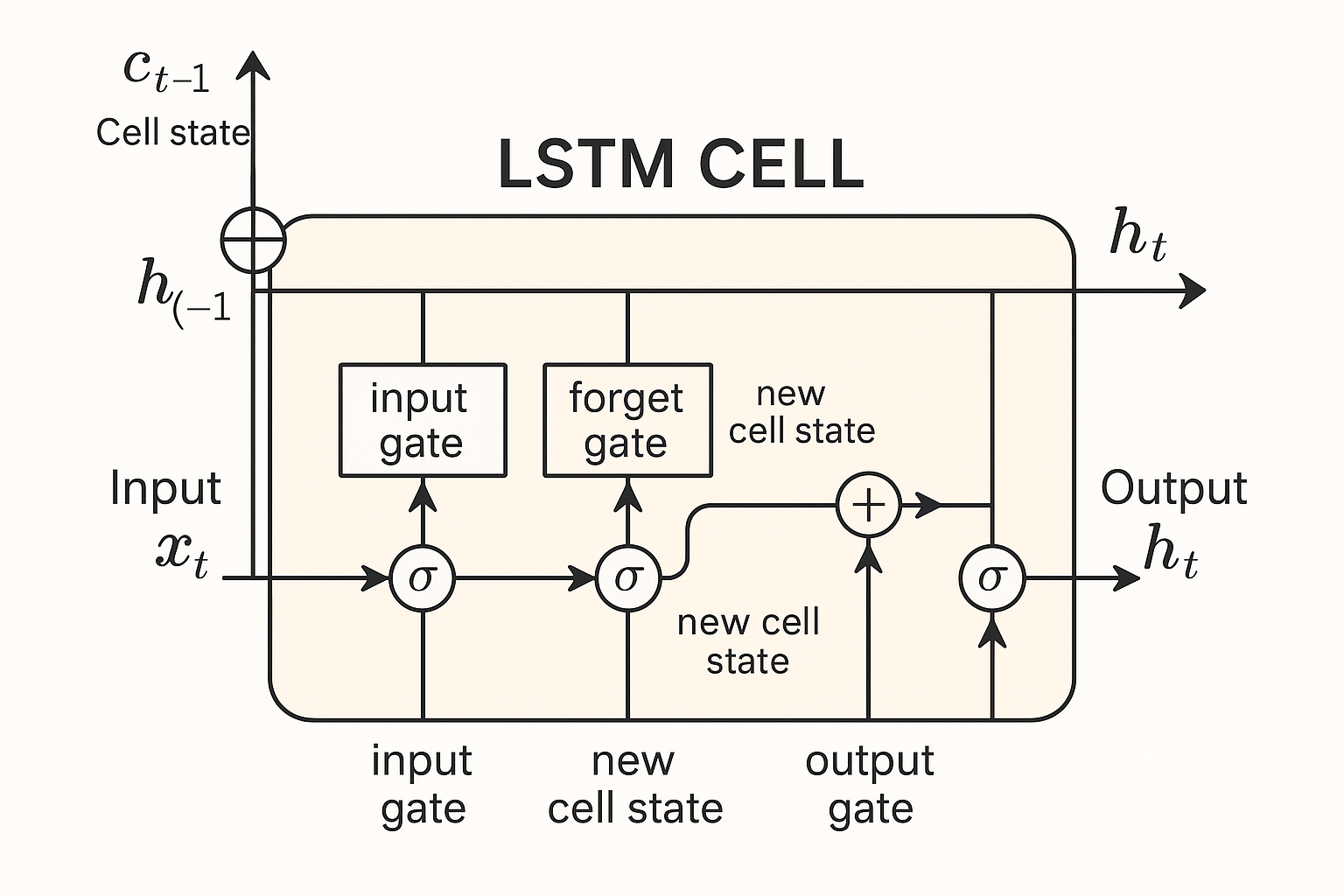
- Forget Gate: The amount of the prior cell state that should be erased or forgotten is determined by this gate. It multiplies the previous cell state element-wise by this output mask after computing a weighted sum of the current input and prior concealed state and passing it through a sigmoid. In order to prevent the vanishing gradient issue during initialisation, the bias of the forget gate is frequently set to values larger than 1.
- Equation: ft = σ(Wf * [ht-1; xt] + bf)
- (where bf is the forget gate bias, [ht-1; xt] indicates the concatenation of the current input and the prior hidden state, Wf is the forget gate’s weight matrix, and σ is the sigmoid function). It is very advised to start the forget gate’s bias term around one during training.
- Input Gate: The amount of the new input that should be added to the cell state is determined by this gate. An input gate and an update candidate (calculated using Tanh) are involved. The amount of the update candidate (tanh) that is written to the memory is managed by the input gate (sigmoid).
- Equation: it = σ(Wi * [ht-1; xt] + bi)
- (where bi is the input gate bias, Wi is the input gate weight matrix, and σ is the sigmoid function).
- Output Gate: At the current time step, this gate regulates the amount of the cell state that is revealed as the hidden state (and frequently the output). It calculates a weighted sum that is passed through a sigmoid and then multiplied element-wise by a cell state that has been changed (passed via tanh).
- Equation: ot = σ(Wo * [ht-1; xt] + bo)
- (where bo is the output gate bias, Wo is the output gate weight matrix, and σ is the sigmoid function).
How it Addresses Vanishing Gradients
Because simple RNNs employ multiplicative updates, gradients may gradually diminish exponentially. In order to solve this, LSTMs update the cell state using an additive architecture. The forgotten part of the previous state and the gated new input are added to the cell state update equation. By making it easier for erroneous gradients to traverse the network over extended periods of time, these additive updates provide the gradient descent process additional stability and information storage persistence.
Equations and Architecture
An LSTM’s state at time t is made up of two vectors: the hidden state h(t) and the cell state c(t). The update equations include element-wise multiplications (⊙) and weighted sums of the current input (x(t)) and the prior hidden state (h(t-1), which are then processed via sigmoid (for gates) or tanh (for candidates). The hidden state (output) is produced using the cell state and the output gate (e.g., h(t) = o ⊙ tanh(c(t))), while the cell state is updated using the forget and input gates (e.g., c(t) = f ⊙ c(t-1) + i ⊙ z where z is the input candidate). Deep LSTMs may be created by stacking many layers.
Variants
The basic LSTM design has several variations, such as the addition of forget gates (which were not included in the initial plan but are thought to be significant) and peephole connections. By processing the input sequence both forward and backward, bidirectional LSTMs (Bi-LSTMs) enable the network to take use of context from both before and after the current word.
Applications
Because LSTMs can manage sequential data and long-term dependencies, they are frequently utilized in NLP. Applications include sequence labelling tasks like named entity identification and part-of-speech tagging, probabilistic language modelling, and auto-regressive text synthesis.
Comparison to Neural Turing Machines (NTMs)
Neural Turing Machines (and Differentiable Neural Computers) are marketed as more sophisticated architectures that explicitly separate external memory from computations, potentially providing better generalizability for tasks requiring controlled memory access over very long sequences, even though LSTMs outperform simple RNNs in memory handling. Memory access and processing are said to be integrated in LSTMs.
