Learn how the Non negative Matrix Factorization algorithm works, its core components like factor matrices W and H, and its applications in text mining, image analysis, and bioinformatics.
Non-negative Matrix Factorization (NMF)
The process of breaking down a non-negative matrix into the product of two non-negative matrices is known as non-negative matrix factorization, or NMF. High-dimensional data can be represented in a lower-dimensional space using this decomposition while retaining the data’s non-negativity.
NLP uses Non-Negative Matrix Factorization to reduce dimensionality and extract features. Latent Dirichlet Allocation (LDA) and Probabilistic Latent Semantic Analysis are often used with this early topic model.
Fundamental Idea:
Decomposition:
Matrix Decomposition NMF is a member of a class of algorithms used in linear algebra and multivariate analysis. Decomposing an original data matrix (usually represented by the letters A or M) into two smaller matrices, W and H, so that the product of W and H is roughly equivalent to the original matrix (A = W × H or M ≈ W × H) is its basic idea.
The Non-Negativity Constraint:
One of the most important aspects of NMF is that all three matrices, the coefficient matrix (H), the feature matrix (W), and the original data matrix (A or M) must only contain non-negative entries. Because of its non-negativity, NMF is especially helpful in applications where non-negative numbers are a natural part of the data.
You can also read Contextual Embeddings: The Word Representations In NLP
Components of the Factorization (A ≈ W × H):
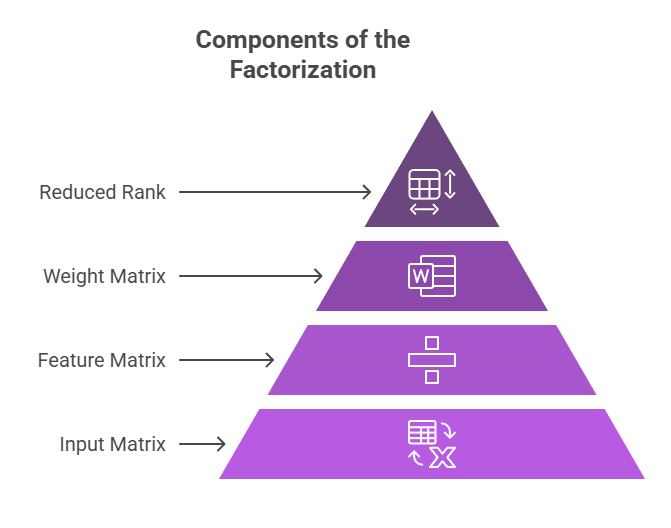
- A (or M): The initial input matrix, in which every element is greater than or equal to 0. This is frequently a document-term matrix in NLP.
- W: The components of the feature matrix or basis. The topic-word distributions, which show the non-negative weight of each word inside each identified topic, can be represented by a document-term matrix.
- H: The weights or coefficient matrix corresponding to W. This can serve as a representation of the document-topic distributions for a document-term matrix, indicating the degree to which each document corresponds to each specified subject.
- k: The reduced representation’s rank or dimensionality. Selecting a lower dimension k (where k ≤ min(dimensions of A)) may help to ignore noise while highlighting important characteristics.
Non negative Matrix Factorization Algorithm
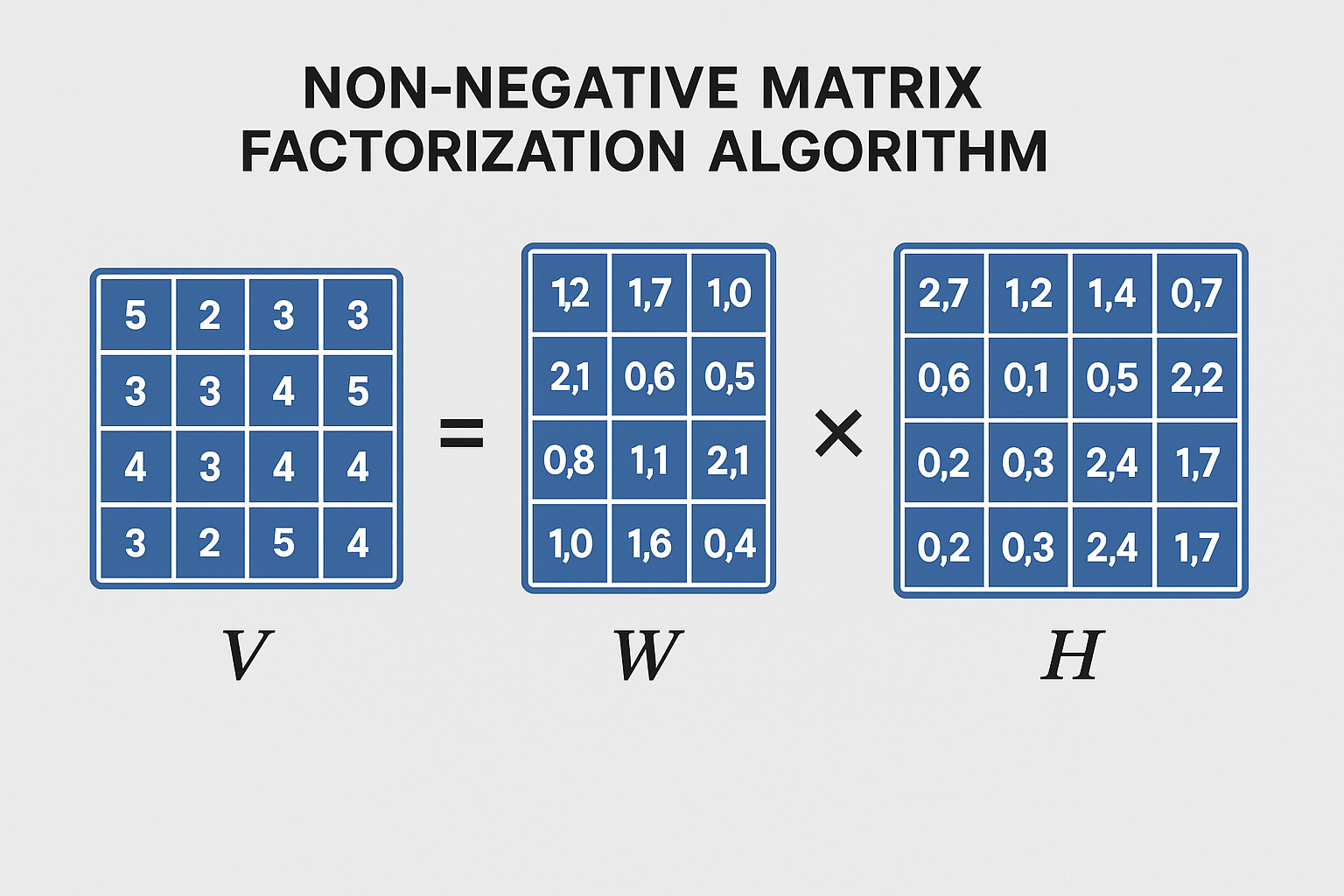
A class of techniques known as non-negative matrix factorization (NMF) is used in linear algebra and multivariate analysis to factor a non-negative matrix V into two non-negative matrices, often W and H. Achieving an approximation where V ≈ WH, where the dimensions of W and H are substantially smaller than those of V, is frequently the aim. By using substantially less data, this approximation seeks to infer some latent structure while representing the elements of V.
NMF algorithms usually minimise a cost function that measures the “divergence” or difference between the original matrix V and the approximation WH in order to identify the non-negative matrices W and H.
There are two typical cost functions in use:
- In order to minimise ‖V − WH‖², the squared error (Frobenius norm) calculates the square of the Euclidean distance between V and WH.
- An expansion of the Kullback-Leibler divergence to positive matrices is known as Kullback-Leibler divergence. The divergence D(V||WH) is measured here.
It is a challenging problem, sometimes referred to as NP-hard, to determine the precise, globally optimal factors W and H. Because they only ensure locating a local, not a global, minimum of the cost function, the majority of existing NMF algorithms are therefore suboptimal.
There are numerous algorithmic methods for carrying out this minimisation:
The Multiplicative Update Rules of Lee and Seung: This well-liked technique is renowned for its ease of use and assured monotonic convergence to a local optimum. W and H upgrades are carried out one element at a time. For two kinds of factorizations based on minimising squared error and Kullback–Leibler divergence, Lee and Seung provided straightforward and practical techniques. It is possible to think of these updates as diagonally rescaled gradient descent.
The updating rules are provided via element-wise multiplication by factors involving expressions such as ((WᵀV)/((WᵀWH)) and ((VHᵀ)/(WHᵀ)) in order to minimise the squared error.
The update rules include element-wise multiplication by factors using words such as (Σᵢ WᵢaVᵢitt)/((WH)itt) and (Σᵢ WᵢaVᵢt*)/(Σk WkaHkt) in order to minimise the Kullback–Leibler divergence.
Alternating Non-negative Least Squares: This method is frequently the foundation of more modern algorithms. Each step involves fixing one factor matrix (W or H) and solving a non-negative least squares problem to find the other. W and H optimisation are switched between in this process. The block primary pivoting method, the optimal gradient method, the active set method, and the projected gradient descent methods are specific techniques that fall under this category.
You can also read SVD NLP: Singular Value Decomposition in NLP
Sequential NMF: Builds each NMF component separately.
Exact NMF: When extra restrictions hold for the matrix V, there are techniques that can determine the exact factorization in polynomial time.
Online NMF: Made for streaming data or enormous datasets that are too big to fit in memory, where the factorization is updated without starting over.
Convolutional NMF: Used to learn features that are equivariant to shifts when input data has spatiotemporal dimensions (such as time signals or images).
Similar to the sparse coding problem, non-negative sparse coding is an NMF problem with an additional L1 regularisation term.
Convex NMF: Prescribes that the input data vectors’ columns must be convex combinations.
When V’s nonnegative rank is identical to its real rank, nonnegative rank factorization, or NRF, is applicable.
The non-negative matrix An extension of Non-Negative Matrix Tri-Factorization (NMTF) divides a matrix into three non-negative matrices.
The algorithm’s final error and rate of convergence are significantly impacted by the initialisation of the factor matrices W and H. Randomisation, SVD, k-means clustering, and more sophisticated techniques are available initialization options.
NLP/Text Mining Application:
NMF works particularly well for text mining. By breaking down a document-term matrix into essential themes, it can be applied to topic modelling in NLP tasks. Latent structure in the data can be found with the use of this decomposition. NMF can generate significant themes, subjects, or patterns by combining attributes. For instance, NMF adds context to text mining by combining phrases like “interest” and “hike” to indicate “interest rates,” or “hike” and “mountain” to propose “outdoor sports.” Additionally, it can be applied to document clustering and content analysis.
Semantic Usefulness of Non-Negativity
Utility Semantically, the non-negativity condition is thought to be helpful, especially in topic modelling. The strength of a topic in a given text can be represented by the non-negative value of each converted feature (for example, in matrix H). This supports the idea that a topic’s presence or contribution shouldn’t be detrimental.
Working of NMF (Iterative Optimization)
Operation to minimise the reconstruction error between the original matrix and the product W × H, NMF breaks down the data matrix using an iterative optimisation procedure. W and H’s values are iteratively changed by the method until their product resembles the original matrix.
- Initialisation: Random non-negative numbers are used to initialise W and H at the beginning of the operation.
- Iterative Update: To reduce the discrepancy (reconstruction error), W and H are changed iteratively. Alternating Least Squares (ALS) and Multiplicative Update Rules (which guarantee non-negativity) are common methods.
- When the reconstruction error stabilises or a predetermined number of repetitions is reached, the procedure comes to an end.
Relationship to Other Methods
The non-negativity constraint is a significant distinction between NMF and other matrix Factorization models, such as Singular Value Decomposition (SVD), which are employed in conventional Latent Semantic Analysis (LSA). It has to do with Probabilistic Latent Semantic Analysis (PLSA), and some sites talk about how NMF and PLSA are equivalent. Neural network designs such as autoencoders can also be used to simulate or implement NMF by factoring a non-negative input matrix roughly with non-linear, non-negative activation functions. Since NMF ensures non-negative solutions, it can be utilised in spectral learning in place of eigendecomposition or SVD. This helps transform solutions into probability vectors.
In conclusion, NMF in NLP is an effective method for breaking down text data (such as document-term matrices) into non-negative elements that stand in for hidden structures like topics. Its main characteristic is the non-negativity restriction on the factorised matrices, which offers a semantically meaningful representation. The strength of topics in documents or words inside subjects can be indicated by the non-negative values. Iterative optimisation is used to minimise the reconstruction error in this method.
You can also read What Is A Radial Basis Function Networks With Example?
