What is a Radial Basis Function (RBF) Networks
In contrast to feed-forward neural networks, radial basis function (RBF) networks are essentially a different design.
- RBF networks map input points into a high-dimensional hidden space, in contrast to feed-forward networks, which transfer inputs forward in a similar manner from layer to layer.
- The main notion is that linear models are enough to represent nonlinearities that existed in the original input space in this higher-dimensional space. This idea stems from Cover’s theorem, which asserts that when pattern classification problems are transformed into a high-dimensional space via a nonlinear transformation, they are more likely to be linearly separable.
- The buried layer calculation, which compares the input with a prototype vector a notion that feed-forward networks lack a perfect equivalent for is where the main distinction is found.
How Do RBF Networks Work?
Although they are implemented differently, RBF Networks and K-Nearest Neighbour (k-NN) models share conceptual similarities. The basic premise is that neighbouring objects with comparable predictor variable values have an impact on an item’s anticipated target value. RBF Networks functions as follows:
- Input Vector: An n-dimensional input vector that requires regression or classification is sent to the network.
- RBF Neurons: A prototype vector from the training set is represented by each neurone in the hidden layer. The Euclidean distance between the input vector and the centre of each neurone is calculated by the network.
- Activation Function: The activation value of the neurone is calculated by transforming the Euclidean distance using a Radial Basis Function, which is usually a Gaussian function. As the distance grows, its value falls exponentially.
- Output Nodes: A weighted sum of the activation levels from every RBF neurone is used by each output node to determine its score. The category with the highest score is selected for categorization.
You can also read Feed Forward Neural Network Definition And Architecture
Architecture
- An input layer, one hidden layer with unique RBF-defined behaviour, and an output layer are the components of a typical RBF network construction. Even if the RBF hidden layer can be followed by more than one feed-forward layer, the network is still shallow in comparison to deep feed-forward networks, and the RBF hidden layer has a significant impact on its behaviour.
- Input Layer: Only sends the hidden layer the input features. The dimensionality of the data is equal to the number of input units. Here, no calculations are made.
- Hidden Layer:
- A prototype vector (μi) is present in every unit in the hidden layer.
- Although the same bandwidth value (σ) is frequently used for all hidden units, each hidden unit also has a bandwidth (σi).
- By comparing the input point (X) with its prototype vector (μi), the hidden layer does calculations. The Gaussian RBF function exp(−||X − μi||² / (2 * σi²)) is commonly used to determine the output of the i-th hidden unit (hi or Φi(X)). Because it decays exponentially, this function only takes on meaningful non-zero values in the small area surrounding the prototype μi.
- Generally speaking, the hidden layer contains more nodes than the input layer. A hyperparameter that is usually greater than the input dimensionality but less than or equal to the number of training points is the number of hidden units (m).
- It is possible to use bias neurones as a unique hidden unit.
- Output Layer:
- Use regression or linear classification depending on the hidden layer’s results.
- Weights (wi) are assigned to connections between the hidden and output layers.
- As a weighted total of the hidden unit outputs, the network’s prediction (Ϸ) is either Ϸ = sum(wi * hi) or Ϸ = sum(wi * Φi(X)).
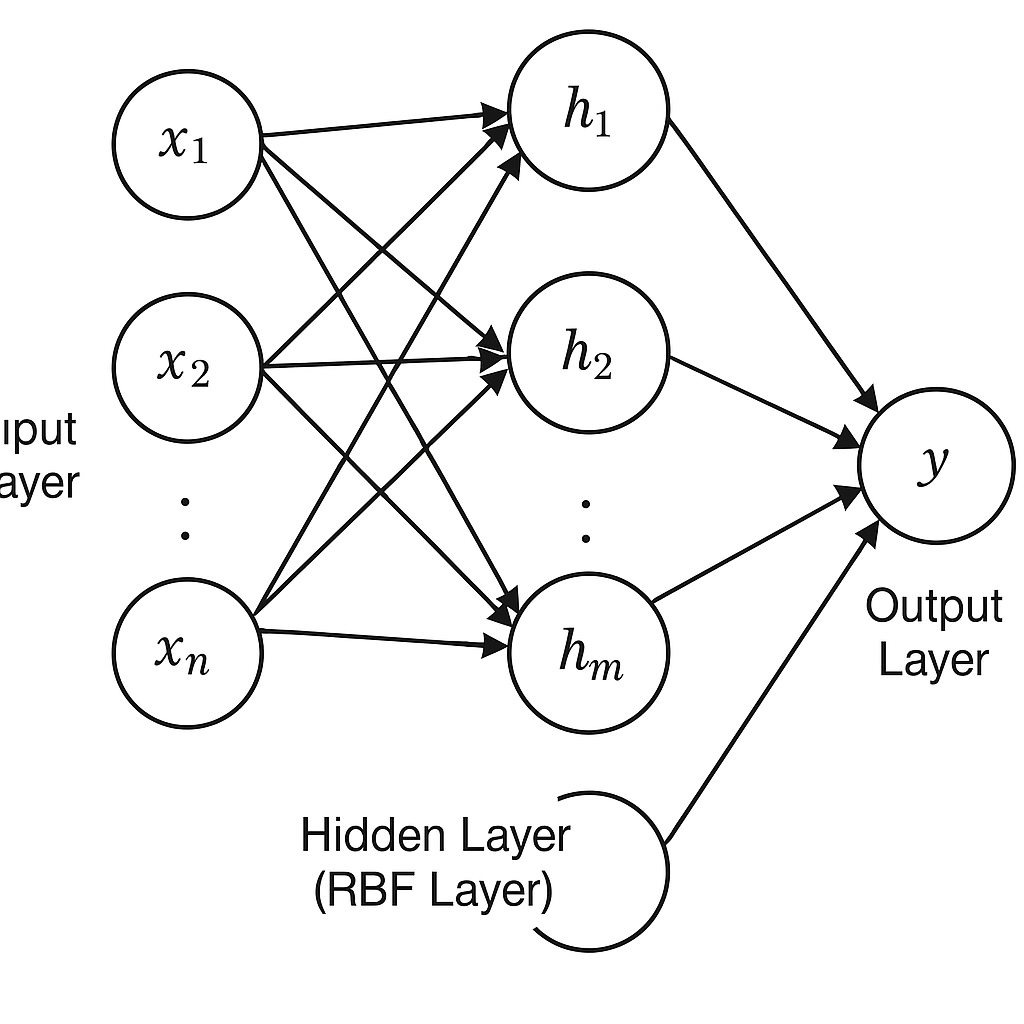
Explanation of Image:
Input Layer
- Nodes labeled x1,x2,…,xnx_1, x_2, \dots, x_nx1,x2,…,xn
- These represent the input features (e.g., words, embeddings in NLP tasks)
- Every input node is connected to each hidden node
Hidden Layer (RBF Layer)
- Nodes labeled h1,h2,…,hmh_1, h_2, \dots, h_mh1,h2,…,hm
- Each of these nodes applies a radial basis function, usually a Gaussian, to compute similarity between the input vector and a learned center (prototype)
- These are the core of the network, acting like soft pattern matchers
Output Layer
- A single node labeled yyy
- It computes a weighted sum of the outputs from the RBF layer
- Often followed by an activation function (like softmax for classification)
You can also read What is Gated Recurrent Unit? What is the purpose of the GRU
Training
- Unlike feed-forward networks, which are trained in a single step, RBF networks are usually trained in two steps.
- Training the Hidden Layer: Typically, the hidden layer’s parameters the prototype vectors μi and bandwidths σi are learnt without supervision.
- Although it is possible to randomly select prototypes μi from the training data, it is common practice to set them to the centroids of clusters (for example, from a k-means clustering technique applied to the training data).
- Bandwidths σi can be chosen depending on the average distance to nearest neighbours or fixed to a given number.
- Although backpropagation (complete supervision) may theoretically be used to train the hidden layer parameters, this method does not appear to be very effective in reality, as it may result in more local minima on the loss surface than feed-forward networks.
- Training the Output Layer: The output layer’s (wi) weights are learnt under supervision. Usually, gradient descent including mini-batch stochastic gradient descent is used for this, or if the output layer has linear activation and minimises squared loss, a linear regression issue is solved (for example, by utilising the pseudo-inverse).
RBF Networks’ Benefits
- Classification: If there are enough neurones, RBF networks may estimate any continuous function with arbitrary precision.
- Regression: When compared to other neural network designs, the training procedure is often quicker.
- Function Approximation: RBF Networks’ simple, three-layer topology facilitates its implementation and comprehension.
Power of RBF networks
- The buried layer’s change encourages linear separability. Classes that are not linearly separable in the input space can be separated using a Gaussian RBF classifier.
- Given enough units, RBF networks may estimate any continuous function using a single hidden layer, making them universal function approximators.
- In contrast to deep feed-forward networks, which largely derive their power from their depth (composition of functions), they derive their strength from the greater number of nodes in the hidden layer (increasing the feature space).
- In contrast to deep feed-forward networks, which are efficient at learning complicated data structures through numerous layers, RBF networks’ single layer restricts the amount of structure that can be learnt.
- RBF networks can withstand some kinds of noise, including adversarial noise, because the hidden layer is trained unsupervised.
You can also read Entity Linking in NLP with Wikipedia, DBpedia, and Freebase
Relationship with Kernel Methods
- RBF networks are seen as straightforward extensions of kernel techniques.
- It can be demonstrated that some RBF network topologies are comparable to well-known kernel techniques:
- Kernel Regression: The prediction function of the RBF network is theoretically equal to that of kernel regression when the prototypes are set to the training points and a fixed bandwidth is employed.
- Kernel Support Vector Machines (SVMs): Similarly, the RBF network produces the same results as a kernel SVM when the prototypes are set to the training points, the same bandwidth is used, and hinge loss is used during training.
- By giving users more control over the amount of hidden nodes and the selection process for prototypes, RBF networks provide greater flexibility than conventional kernel approaches, potentially improving accuracy and efficiency. By selecting a suitable loss function, they may replicate almost any kernel technique.
Applications
- RBF networks are useful for linear interpolation, regression, and classification.
- They were originally employed in the last layer of character recognition systems such as LeNet-5, where the RBF units matched the output vector of the network to manually selected character class prototypes (although this particular application is now seen as outdated).
- They may be used for semi-supervised classification and unsupervised outlier identification.
Current Status
- RBF networks are referred to be a “forgotten category” of neural architectures because of their little usage in recent years, despite its potential and connection to kernel approaches.
- They still have a lot of promise, though, in situations where kernel approaches are useful. By include layers following the first RBF hidden layer, they may also be integrated with feed-forward systems.
Radial Basis Function Example
Think of a dataset that contains two-dimensional data points from two different classifications. Each of the 20 neurones in an RBF network that has been trained will represent a prototype in the input space. 3-D mesh or contour plots can be used to visualise the category scores that the network calculates. Neurones in the same category are given positive weights, whereas neurones in separate categories are given negative weights. Plotting the decision border involves analysing scores over a grid.
You can also read An Introduction To Restricted Boltzmann Machines Explained
