SVD NLP
Singular Value Decomposition (SVD) is a potent algebraic method mostly used for matrix factorization and dimensionality reduction in Natural Language Processing (NLP). The goal of this technique is to find low-dimensional representations of high-dimensional data that retain the majority of the original data’s information. SVD can use co-occurrence analysis to extract semantic information.

A matrix M, which usually represents linguistic data such as a word-document matrix or a word-context matrix, is factorized into three additional matrices via SVD:
M = U Σ V^T
This is where:
In a m × n matrix, for example, where m could represent the number of terms and n the number of documents, or vice versa, M is the original matrix.
The matrix U is m × r. Each of its columns is orthonormal.
Σ (Sigma) is a diagonal matrix of size r × r. On its diagonal, the singular values of M are the non-zero elements. It is customary to arrange these singular values in descending order.
Considering that V is a n × r matrix, V^T is a r × n matrix. The rows of V^T, or columns of V, are orthonormal.
The rank of matrix M is denoted by r. Factorization is accurate.
Dimensionality Reduction with Truncated SVD
The singular values in Σ represent the degree of variance along corresponding dimensions, which is the source of SVD’s power for dimensionality reduction. We can approximate the original matrix by retaining only the top k largest singular values and their corresponding columns from U and V, as they are arranged in order of importance. This type of approximation is known as low-rank or shortened SVD.
To reduce the dimensionality to k (k < r), we retain only the first k columns of U (Uk), the first k diagonal elements of Σ (Σk), and the first k rows of V^T ((Vk)^T).
The resulting matrix product M_k = Uk Σk (Vk)^T is the closest approximation of M of rank k as measured by the Frobenius norm.
This lower-rank matrix M_k can be seen as a “smoothed” version of the original data, capturing the most important patterns.
Contextual Interpretation in NLP
Applying SVD to a word-context matrix or a term-document matrix (where inputs may be TF-IDF scores) yields numerical representations:
- For terms or words, the rows of the reduced U matrix (which has k columns) can be used as k-dimensional vector representations. In the original data, these packed vectors capture the most significant directions of variance.
- While the method does not always ensure this interpretation, it is possible to read the columns of U as semantic dimensions or subjects.
- In the new k-dimensional space, the documents or contexts can be represented similarly by the rows of the reduced V^T matrix.
- When words or documents that had similar co-occurrence patterns in the original high-dimensional space are projected into a lower-dimensional space, they will be mapped closer together in the reduced space, making them more similar.
Uses for Natural Language Processing
SVD is frequently used in NLP activities as a component of Latent Semantic Analysis (LSA):
- SVD is used to factor term-document matrices in the well-known application of Latent Semantic Analysis (LSA). LSA factors matrices of word and context counts to produce continuous vector representations of words. It is employed to improve information retrieval by matching ideas rather than just keywords, discover latent concepts in document collections, and derive semantic information (such as synonymy and polysemy).
- Word Sense Disambiguation (WSD): By reducing the dimensionality of context vectors, SVD addresses the problem of sparse data and enhances word sense separation by clustering.
- Information Retrieval (IR): SVD is utilized with term-document matrices in IR systems, which go beyond LSA. Distributed search and query categorization are two applications of LSI (based on SVD).
- Dimensionality Reduction: SVD is a broad technique used in areas like text visualization and compression where it is advantageous to reduce the number of features.
- The use of neural networks and machine learning
- It is demonstrated that SVD is theoretically identical to shallow autoencoder neural networks. This makes neural network structures easier to comprehend as extensions of traditional techniques.
- SVD can be applied to neural network weight initialization or to related methods such as feature pre-processing whitening.
- Autoencoder variations that are related to regularized SVD include contractive autoencoders and de-noising autoencoders.
- Word Embeddings: Although Word2vec takes a different approach, the idea of learning dense word vectors is related to matrix factorization methods such as SVD when they are used on altered co-occurrence matrices (such as PMI-weighted matrices).
- SVD and Principal Component Analysis (PCA) have a close relationship. Applying SVD on a mean-centered matrix is the same as PCA. Finding the axis of greatest variation and reducing dimensionality are two uses for both.
Limitations
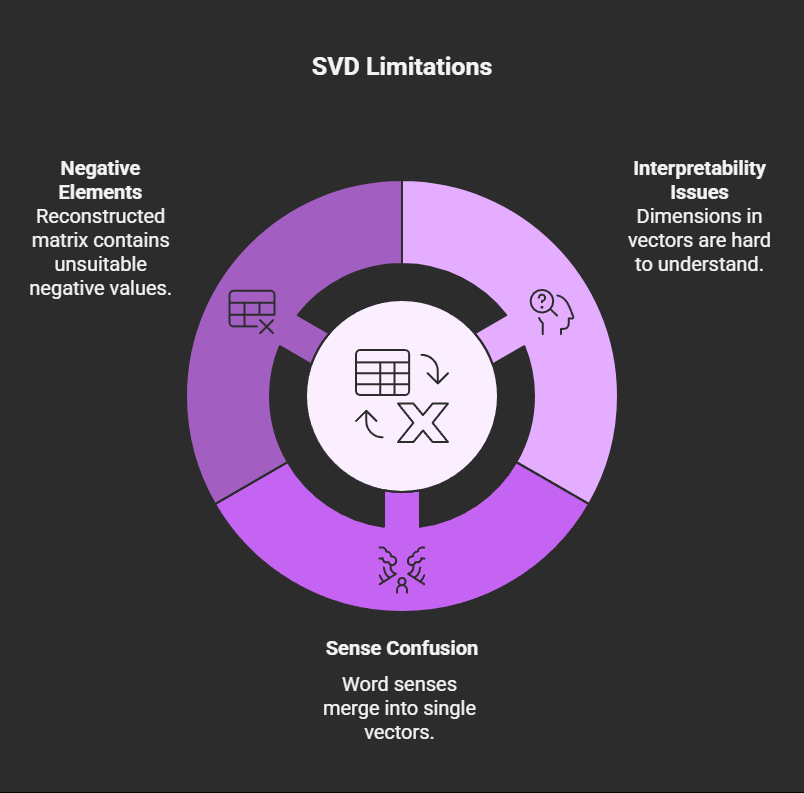
SVD is useful, however it has certain drawbacks:
- It is not always possible for people to directly interpret the dimensions in the generated vectors.
- SVD can confuse various word senses into a single vector representation when used on word representations, which can be troublesome for applications that need for precise meaning distinctions.
- Sometimes the reconstructed matrix contains unsuitable negative elements when counts are estimated using a low-rank approximation.
