What is Neural Turing Machine (NTM)?
An artificial neural network that combines traditional neural networks with memory features akin to those of a Turing machine is called a Neural Turing Machine (NTM). Inspired by the human brain, it is intended to develop learning algorithms that can be run on general-purpose computing devices. In 2014, Alex Graves, Greg Wayne, and Ivo Danihelka of DeepMind Technologies presented the NTM architecture.
NTMs’ primary objective is to improve neural networks’ capacity for data storage, manipulation, and retrieval so that they can tackle challenging problems involving algorithmic processing and logical reasoning. Similar to a Turing machine or Von Neumann architecture, the combined system can be effectively trained using gradient descent since it is end-to-end differentiable.
History
Neural networks were generally seen as an unpromising avenue for the first thirty years of artificial intelligence (AI) development, with symbolic AI predominating from the 1950s until the late 1980s. In 1986, a noteworthy substitute known as Parallel Distributed Processing (or connectionism) with artificial neural networks surfaced.
Neural networks have been criticised for their ability to comprehend intelligence in two major ways:
- They appeared unable of resolving issues involving inputs of changing sizes. Recurrent neural networks (RNNs) were developed in order to address this.
- They seemed to lack the “variable-binding” capability, which is essential for information processing in computers and brains and involves tying values to particular locations in data structures.
By giving a neural network an external memory and the ability to learn how to use it, Graves et al. sought to answer this objection; they dubbed their system a Neural Turing Machine.
The architecture of the NTM was greatly impacted by the idea of working memory, which is defined in psychology, linguistics, and neuroscience as the short-term storage and rule-based manipulation of information. The NTM is similar to a working memory system because it is made to handle problems that involve using “rapidly-created variables” to apply approximate rules.
The first stable open-source implementation was released at the 27th International Conference on Artificial Neural Networks in 2018 and won a best-article award, despite the fact that the original NTM study did not share source code.
Also Read About What is Gated Recurrent Unit? What is the purpose of the GRU
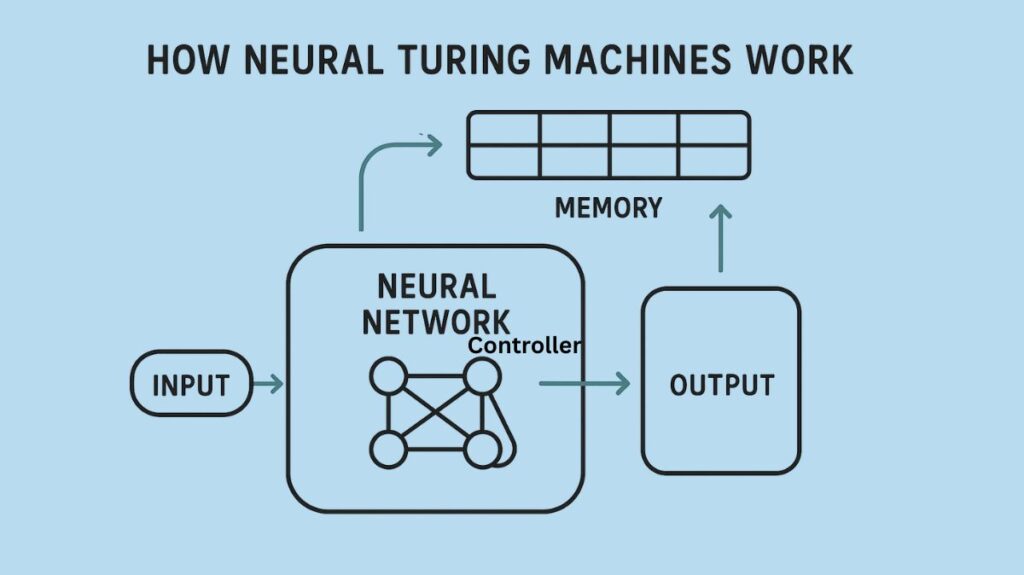
How Neural Turing Machines Work
Components
There are two key components that make up an NTM:
- Controller: This is the main neural network that learns to read from and write to the memory matrix. It is frequently a feedforward network or a recurrent neural network (RNN). It works similarly to a computer’s processor.
- Data is stored in a two-dimensional array, often referred to as a memory matrix or memory bank. Selective read and write operations enable the controller to communicate with this memory.
The controller uses specialized outputs known as “heads” to communicate with the memory matrix. Among these heads are:
- Read Heads: Parts that allow the controller to access data stored in designated memory regions.
- Write heads are the parts that enable the controller to update or store data in the memory matrix.
Importantly, the emphasis of the read and write heads on the memory matrix is determined by attention mechanisms, which function as soft addressing systems. This enables content or location-based memory access for the NTM.
Operations
NTMs use a series of actions that include writing to and reading from the memory matrix. The controller gets input at each time step and determines the read and write operations based on its current state. Selective reading and writing are made possible by the attention mechanisms, which assist the controller in concentrating on particular areas of the memory. Then, using the collected data and the controller’s state, the NTM’s output is calculated.
One revolutionary feature of NTMs is that they can be trained end-to-end using gradient descent and backpropagation because the entire system is differentiable. Instead of addressing a single memory element exactly like a conventional Turing machine, this is accomplished by defining “blurry” read and write operations that interact to varied degrees with every memory element. A method of attentional “focus” determines the “blurriness” by limiting each operation to interacting with a limited amount of memory.
Also Read About Deep networks and Deep Networks Challenges
Addressing Mechanisms
In order to create weight vectors that specify where to read from and write to, the “blurry” read and write operations use a four-step procedure. These weight vectors, which show how much a head interacts with each memory location, are normalized, meaning that their elements range from 0 to 1 and add up to 1.
The following are the two complementary addressing mechanisms:
Content-based addressing
The first is content-based addressing, which directs attention to memory regions according to how closely their present values match a “key vector” that the controller emits. The “key strength” option establishes the level of concentration required for this focus. This enables the controller to retrieve values that are comparable to those that have been seen before.
Location-based addressing
This technique enables random-access jumps as well as basic iteration over memory regions. It is vital for jobs where a variable’s constant position is critical but its content is random, like in arithmetic operations where values ‘x’ and ‘y’ are kept at specified addresses.
To create a weight vector, follow these four steps:
- Content Addressing: Creates a content weight vector by comparing each memory row to a key vector from the controller.
- Interpolation: The “interpolation gate,” a scalar parameter, combines the content weight vector with the weight vector from the prior time step, enabling the system to learn when to employ or disregard content-based addressing.
- Convolutional Shift: A normalised distribution over permitted integer shifts (such as +1, 0, and -1) is defined by the “shift weighting” that each head emits. This enables the controller to do circular shifts and move focus to other rows.
- Sharpening: To keep the focus on memory locations crisp over time, a scalar parameter is utilized to stop the shifted weight from blurring.
Flexible data access is made possible by the integrated system’s three operating modes: content-based just, content-based then shifted, or previous weighting rotated without content input.
Features
- Blends Pattern Matching and Algorithmic Power: NTMs fill the gap between programmable computers’ algorithmic power and neural networks‘ fuzzy pattern matching.
- Differentiable End-to-End: The NTM architecture as a whole is differentiable, which makes gradient descent training effective.
- Acquires the Ability to Utilise External Memory: NTMs are built with the ability to store, modify, and access data from an external memory matrix.
- Infers Simple Algorithms: From input and output samples, NTMs are able to directly infer simple algorithms like copying, sorting, and associative recall.
- Generalisation: One of the main characteristics of NTMs is their capacity to apply learnt algorithms far outside of the scope of their training data; for example, they can replicate sequences that are far longer than those observed during training.
Types (Controller Types)
One important architectural decision is the kind of neural network that is employed as the controller. In particular, sources contrast two kinds of controllers:
- Feedforward Controller: By reading and writing at the same memory address at each stage, this kind of controller can simulate a recurrent network. Because memory access patterns are simpler to understand than an RNN’s internal state, it frequently offers more transparency in the network’s functioning. One drawback, though, is that the quantity of read and write heads operating simultaneously may cause a computational bottleneck.
- LSTM Controller: An LSTM network controller can supplement the bigger external memory matrix with its own internal memory. This eliminates the bottleneck caused by the number of heads, unlike feedforward controllers, and enables the controller to blend data across several time steps.
Advantages
Compared to typical neural networks, especially recurrent neural networks like LSTMs, NTMs have the following advantages:
Overcomes traditional Neural Network Limitations
NTMs are made to overcome the difficulties that traditional neural networks encounter when storing and manipulating data for prolonged periods of time.
Better Algorithmic Task Performance
In a number of tests, NTMs performed noticeably better than LSTMs on tasks involving algorithmic processing and long-term memory, including:
- Copying: NTMs shown a significant improvement in problem-solving skills, learnt far more quickly, converged to lower error rates, and were able to generalise to far longer sequences than those they were trained on.
- Repeat Copying: NTMs demonstrated the capacity to learn basic nested functions by learning this task significantly more quickly and completing more repetitions than LSTMs.
- Associative Recall: NTMs learnt this job far more quickly than LSTMs, and feedforward-controller NTMs even outperformed LSTM-controller NTMs. This suggests that NTMs are a better data storage system because of their external memory. Additionally, they were better at generalising to larger item sequences.
- Dynamic N-Grams: When it came to quickly adjusting to novel predictive distributions, NTMs outperformed LSTMs by a tiny but noteworthy margin.
- Priority Sort: When learning to sort data according to priority ratings, NTMs performed noticeably better than LSTMs.
Acquires Generalisable Algorithms
Compared to Long Short-Term Memory(LSTMs), NTMs exhibit the capacity to acquire a greater number of generalizable algorithms.
Simplified Neural Models
The Evolvable Neural Turing Machine (ENTM), an evolvable variant of NTM, can significantly simplify neural models and improve generalisation.
Disadvantages of neural turing machines
NTMs still have several drawbacks despite their improvements:
- Complexity and Cost of Computation: Because of the complicated interconnections between the memory and the controller, training NTMs can be both complex and costly.
- Attention Mechanism Design and Tuning: Careful thought must go into creating and adjusting the attention mechanisms for certain jobs.
- Implementation Stability: Some open-source NTM implementations were not robust enough for production use as of 2018. Issues like gradients turning “NaN” (Not a Number) during training, which results in training failure, or sluggish convergence were raised by developers.
- Memory Size Limitation: Because cyclical shifts may overwrite previously stored data, the external memory’s size may be a limiting factor for operations like duplicating lengthy sequences.
- Generalization of Numerical Repetitions: When the number in the repeat copy task was represented numerically, NTMs found it difficult to generalize counting repetitions, which resulted in inaccurate end marker predictions outside of the training range.
Also Read About Bidirectional LSTM vs LSTM Key Differences Explained
Neural Turing machine Applications
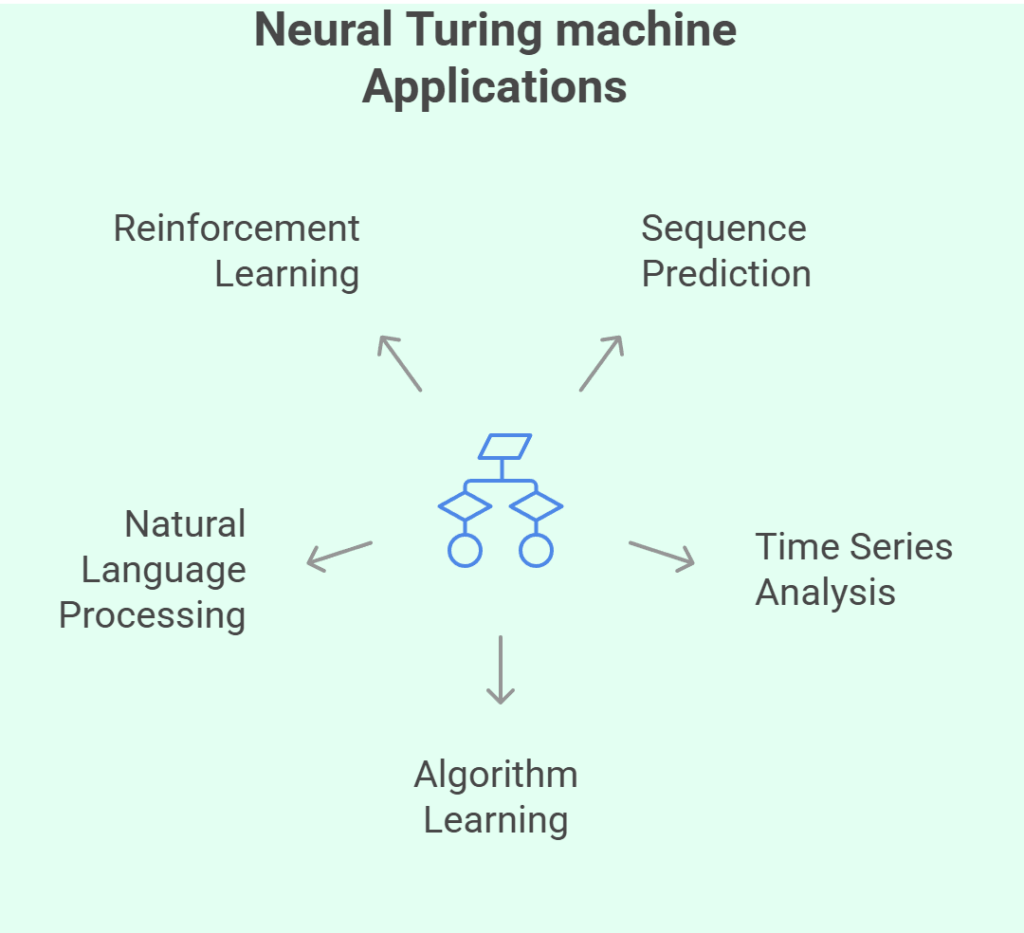
Potential uses for neural Turing machines include fields requiring the solution of algorithmic or procedural problems:
- Predicting subsequent items in sequences that adhere to intricate patterns or rules is known as sequence prediction.
- Time Series Analysis: Time series jobs need the storage and manipulation of temporal data.
- Algorithm learning is the process of reproducing and extrapolating algorithms from sample input-output pairs.
- Natural Language Processing: By preserving state information throughout lengthy texts, this technique may improve language models.
- Reinforcement learning is the process of using memory to recall and make sense of previous behaviours and conditions in reinforcement learning settings.
Related Concepts
NTMs rely significantly on a number of fundamental ideas:
- Turing Machine: A computational model in theory. Turing’s idea of adding an infinite memory tape to finite-state computers is the inspiration behind the moniker of NTMs.
- Von Neumann Architecture: A form of computer architecture that integrates memory and processor.
- Working Memory: An important source of inspiration for NTMs, working memory is a psychological and neuroscience concept involving the manipulation and storage of short-term information.
- Recurrent Neural Networks (RNNs): A dynamic state class of neural networks that can analyse inputs of varying lengths and perform intricate data transformations over time. In theory, RNNs are known to be Turing-Complete.
The “vanishing and exploding gradient” problem was addressed by the development of Long Short-Term Memory (LSTM), a significant advancement in RNNs that embeds integrators for memory storage. LSTMs are frequently used as controllers for NTMs.
Prospects for the Future
Potential areas of future NTM study include:
- Enhancing training techniques.
- Investigating various controller kinds.
- Looking for scalable and more effective methods to carry out memory operations.
