What are Generative Stochastic Networks?
A generative probabilistic model known as a Generative Stochastic Network (GSN) offers an alternative to conventional Unsupervised Learning techniques. GSNs use a Markov chain to learn to model a generative process, as opposed to models that explicitly estimate the probability distribution of inputs.
Generative Stochastic Networks (GSNs) are a type of generative model introduced by Yoshua Bengio and colleagues in 2014. GSNs are designed to learn a data distribution and generate new samples from it similar in spirit to autoencoders and energy-based models.
A framework for training generative models to select samples from a desired distribution is called a Generative Stochastic Network (GSN). Because such machines may be made to be trained by back-propagation, this method has advantages.
Core Concept: Learning the Transition Operator
Training a network to learn the transition operator of a Markov chain is the main concept behind GSNs. The aim is for the stationary distribution of this Markov chain to approximate, or provide a reliable approximation of, the distribution of the data.
A Markov chain is a series of random variables in which the previous events’ sequence has no bearing on the future state; only the current state does.
Moving from one state to another is defined by a function called the transition operator. This operator is parameterized by a Neural Networks in a GSN.
The long-term probability distribution of the Markov chain is known as the stationary distribution. This distribution should converge to the distribution of the data that was used to train the GSN if it is properly trained.
A complex unsupervised density estimation problem is reduced to a more manageable supervised function approximation problem by GSNs, which learn a simpler conditional transition distribution rather than the full data distribution directly. Since the transition distribution usually consists of short moves, learning is made easier because it has fewer dominating modes and becomes unimodal at the small move limit.
How Generative Stochastic Networks Work?
Generalization of Denoising Auto-Encoders (DAEs)
In the GSN framework, Denoising Auto encoders are generalized. By offering a probabilistic interpretation for DAEs, it demonstrates how auto-encoders trained with injected noise can be viewed as generative models and considered a specific case of GSNs.
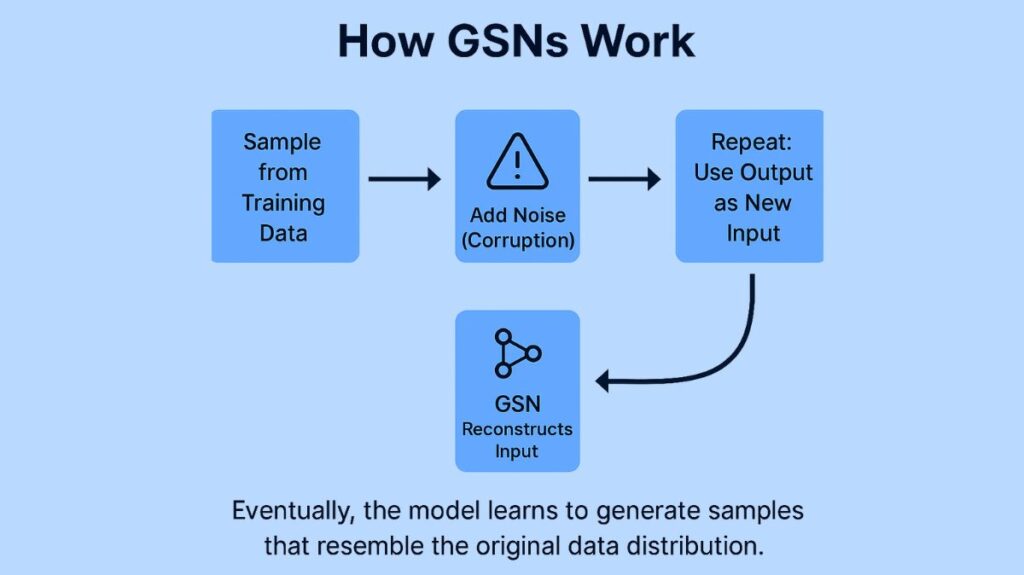
It is possible to think of a basic GSN as an iterative process:
- Corrupts the Data: Noise is purposefully added to a clean data sample taken from the training set.
- Reconstructs the Data: The function of the network is to “denoise” or reconstruct this tainted sample into a clean one.
- Iterates the Process: The Markov chain starts with this reconstruction. The sample is then corrupted and reassembled one more before being used as the input for the next stage.
After a number of steps, the network learns to do this denoising/reconstruction so well that the generated samples will eventually look like they came from the original, clean data distribution. This is because the network is forced to discover the underlying structure and relationships of the data by the training objective.
Key Characteristics
Training with Backpropagation: Standard backpropagation can be used to train GSNs, which is a major advantage. Intractable computations (such calculating a partition function) and other computational difficulties that come with conventional generative models are avoided in this way. The gradients are acquired without layerwise pretraining by backpropagating through a Recurrent Neural Networks with injected noise.
Modeling Flexibility: In addition to observable random variables (x), GSNs can also include arbitrary deep structures and latent (or hidden) variables (h) in the Markov chain, which enables them to capture more sophisticated and potent data representations.
Handling Missing Data: In addition to sampling subsets of variables given the others, the system is well-suited for managing missing inputs.
Theoretical Justification: Even in cases when conditional distributions are contradictory, the theorems underlying GSNs provide an intriguing defense of dependency networks and generalized pseudolikelihood by establishing a suitable joint distribution and sampling mechanism.
Comparison to Other Models
Generative Adversarial Networks (GANs): The adversarial nets framework does not require a Markov chain for sampling, in contrast to Generative Stochastic Networks. Additionally, because GANs do not require feedback loops during generation, they are better able to utilize piecewise linear units, hence avoiding problems with unbounded activation.
Directed Graphical Models (such as RBMs and DBNs) with Latent Variables: During maximum likelihood estimation, these models frequently require unmanageable probabilistic calculations, which GSNs seek to avoid. Back-propagation is used to train GSNs, in contrast to many RBM-based models.
Graphical models that are not directed, such as RBMs and DBMs: These models frequently have intractable partition functions, and Markov Chain Monte Carlo (MCMC) methods—which may have mixing issues are used to estimate their gradients. In contrast, GSNs do not require Markov chains for post-training sampling because they are trained using back-propagation.
Other Generative Models: Recent instances of back-propagating into a generative machine for training include stochastic backpropagation and Auto-Encoding Variational Bayes (AEVB), in addition to Generative Stochastic Networks. For example, AEVB uses stochastic gradient techniques to focus on effective inference and learning in directed probabilistic models with continuous latent variables and intractable posterior distributions.
Advantages of Generative Stochastic Networks
No Need to Compute Partition Function
GSNs are simpler and quicker to train than energy-based models (like RBMs) since they do not have to deal with the intractable partition function.
Extends Autoencoders with denoising
By extending denoising autoencoders to develop generative models, GSNs are able to sample fresh data in addition to reconstructing it.
Conceptual Promises
Provable consistency is provided by the convergence of the Markov chain specified by the GSN to the data distribution under specific conditions.
Modular and Flexible
Modular and Flexible GSNs enable modular design, which enables the plugging in of different architectures (such as CNNs and deep neural networks).
Acquiring Knowledge Without Explicit Probability
Instead of calculating log-likelihoods, which is helpful when likelihoods are difficult to define or calculate, GSNs learn by sampling and reconstruction.
Disadvantages of Generative Stochastic Networks
Training is Still Challenging
Even though GSNs are easier to train than RBMs or DBNs, the network architecture and noise model still need to be carefully planned.
Sampling Slowly
Compared to VAEs or GANs, GSNs generate more slowly because they rely on a Markov chain, which may require a lot of steps to mix properly.
Limited Tooling and Adoption
GSNs are less popular than GANs and VAEs, which translates to fewer libraries, examples, and community support.
Corruption Process Sensitivity
Selecting an efficient corruption (noise) process is essential to the model’s success. Bad decisions might hinder convergence or degrade performance.
Scaling to high dimensions is more difficult.
Similar to many early generative models, GSNs may have trouble processing complex or high-dimensional input, particularly when contrasted with more recent models such as transformers or diffusion models.
Applications and Examples
Despite providing significant theoretical foundations, GSNs were mostly used in:
- Unsupervised Learning: Finding the data’s underlying structure without the use of labels.
- Image Generation: Creating fresh pictures that are comparable to the training set.
- Denoising and Reconstruction: Tidying up noisy photos or filling in the gaps in the data.
GSNs’ theoretical outcomes have been verified by experiments, which have demonstrated success on both synthetic and picture datasets. In particular, the study notes that two image datasets were used for validation. These experiments’ architecture mimicked the Gibbs sampler included in a Deep Boltzmann Machines.
Researchers Guillaume Alain, Yoshua Bengio, Li Yao, Jason Yosinski, Éric Thibodeau-Laufer, Saizheng Zhang, and Pascal Vincent, who were connected to Cornell University and the University of Montreal, were among those who first introduced GSNs.
It should be noted that although GSNs offered important theoretical underpinnings and encouraging outcomes, especially in image processing and denoising, more recent and extensively used generative models such as Generative Adversarial Networks and Variational Autoencoders have largely surpassed them in real-world applications. However, GSNs continue to play an important role in the development of deep generative models, and previous studies have been impacted by their fundamental ideas.
