A notable development in deep learning, Spatial Transformer Networks (STNs) are mainly intended to improve the spatial invariance of computer vision systems. They are a specific kind of Convolutional Neural Network (CNN) that can actively change the input data’s spatial dimensions inside the network. This feature enables a neural network to learn how to enhance spatial invariance by performing spatial modifications on input data.
What is Spatial Transformer Networks?
What are Spatial Transformer Networks?
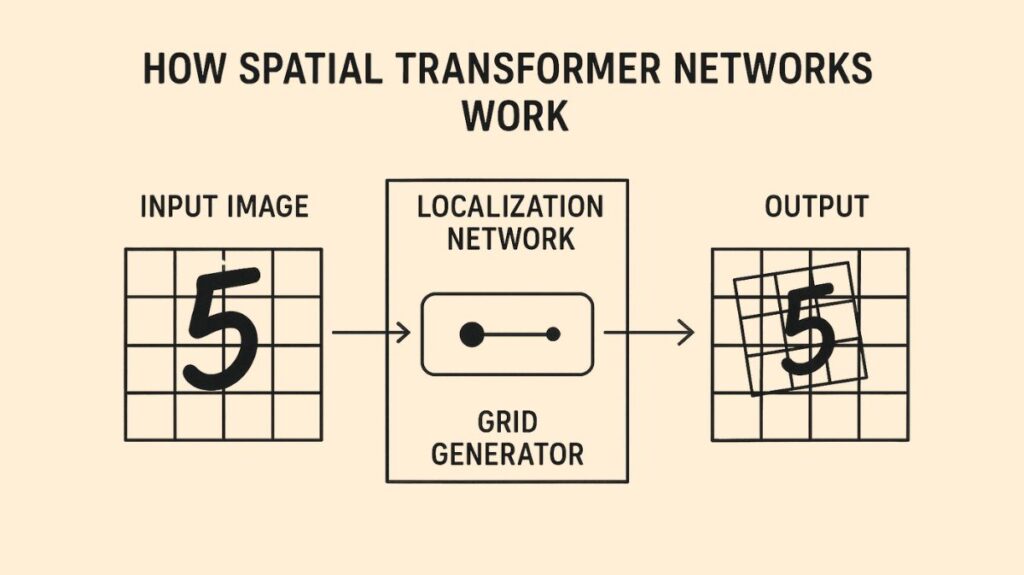
Neural networks may actively and spatially change feature maps conditional on the feature map itself by integrating learnable modules called Spatial Transformer Networks (STNs) into pre-existing convolutional architectures. Regardless of spatial transformations like translation, scaling, rotation, cropping, or non-rigid deformations like elastic deformations, bending, shearing, or other distortions, they seek to enable a computer vision system to recognize the same item. STNs improve object classification and identification by stabilizing or enhancing an item in a processed picture or video.
Traditional CNNs are powerful but inefficient at spatial invariance. Local max-pooling layers provide some spatial invariance, but only across a deep hierarchy and are limited by pooling operations’ narrow spatial support (2×2 pixels). This implies that CNN intermediate feature maps are not invariant to massive input modifications.
History
A 2015 paper titled “Spatial Transformer Networks” by Max Jaderberg et al. introduced the idea of spatial transformer networks. By explicitly enabling geographical data modification within the network, this innovative architecture improves the capabilities of the model.
How Spatial Transformer Networks Work (Functionality and Architecture)
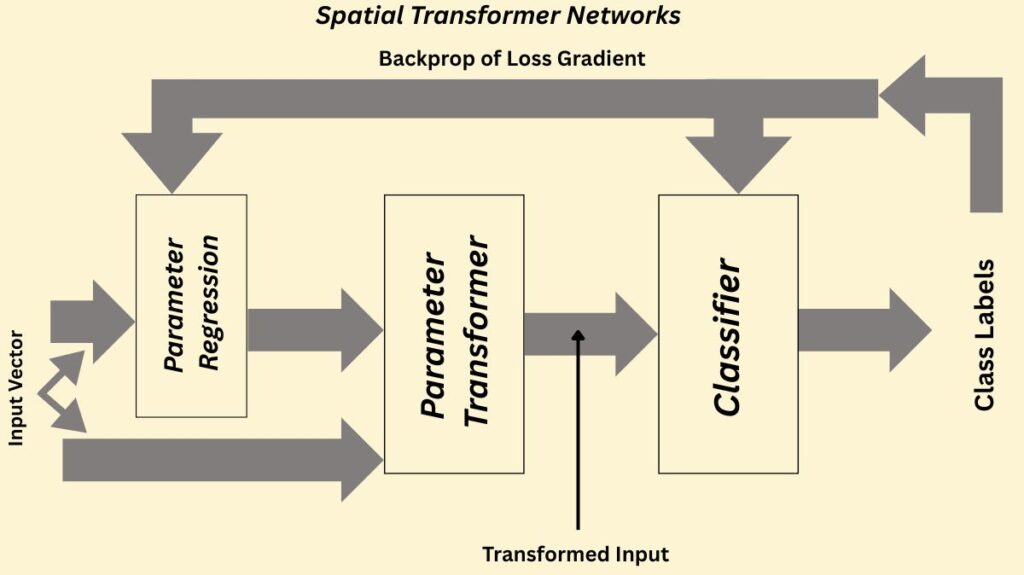
The spatial transformer module is the main part of a STN. This module improves accuracy and efficiency by operating with a separation of concerns, where each component fulfils a specific function. Backpropagation is used to train the complete STN architecture from beginning to end. This enables the network to learn the classification and the spatial transformation parameters at the same time without the need for additional training supervision or changes to the optimization procedure.
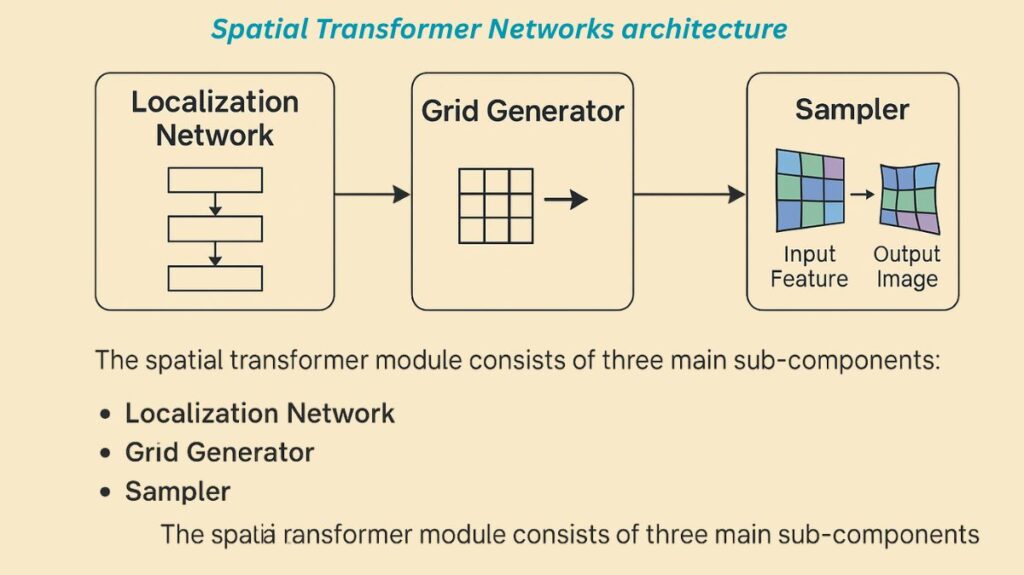
The spatial transformer module consists of three main sub-components:
Localization Network: This sub-network determines the parameters that will convert the input feature map into a standard, canonical pose. Convolutional and fully-connected layers that learn to regress these transformation parameters are usually included. The intricacy of the transformation determines how many dimensions are required for these parameters; for instance, a straightforward translation may need two dimensions, but a more intricate affine transformation may need as many as six. This network can be convolutional or fully-connected, but it needs to have a final regression layer to provide the transformation parameters.
Grid Generator: The grid generator employs reverse mapping to extrapolate a sample grid for the input image using the inverse of the transformation parameters from the localization network. The exact, frequently non-integer, places in the image that will be used to sample pixel values to create the output image are specified by this grid. Based on the transformation settings, the grid generator generates a grid of coordinates in the input data that match the output.
Sampler: The grid generator sends the sampling grid, or set of coordinates, to the sampler. After that, it uses bilinear interpolation to extract the matching pixel values from the input map. Finding the four nearby points around a corresponding output point, weighing each one according to proximity, and then mapping the output point based on the findings are the steps in this method. To maintain spatial consistency, the sampling is applied in the same way for every channel of a multi-channel input (such as RGB pictures). Because this component is differentiable, gradients can return to the sample grid coordinates and the input feature map, and then to the transformation parameters and localization network.
Types of Transformations
Spatial Transformer Networks can learn invariance to a wide range of spatial transformations:
- Translation
- Scale (isotropic and non-isotropic)
- Rotation
- Cropping
- More general affine transformations (including shearing)
- Non-rigid transformations such as elastic deformations, bending, or other distortions
- Projective transformations
- Piece-wise affine transformations
- Thin plate spline transformations
Features
Differentiable Module: Because Spatial Transformer Networks are differentiable, normal backpropagation can be used to train them end-to-end without changing the optimization procedure.
Flexible Input/Output Sizes: STNs are capable of processing inputs of any size and generating outputs that are distinct from one another. They can also define multiple output dimensions to either oversample or downsample a feature map.
Parallel Processing: Like max pooling, the division of labor permits effective backpropagation and lowers computing overhead. Additionally, it makes it possible to calculate numerous target pixels at once, which speeds up the process by using parallel processing.
Multi-Channel Inputs: By using the same mapping procedure for every channel to maintain spatial consistency, STNs offer a sophisticated solution for multi-channel inputs, such as RGB color images.
Integration Flexibility: Spatial transformer networks are created by dropping self-contained modules called spatial transformers into a CNN design in any number and at any moment. More abstract representations can be transformed by positioning several STNs at progressively deeper depths. For tasks requiring several objects or areas of interest, numerous STNs can also be utilized concurrently.
Advantages and Benefits
Improved Spatial Invariance: STNs greatly increase spatial invariance, which enables networks to identify objects in spite of changes in position, orientation, scale, and other transformations.
Enhanced Performance: They address a persistent flaw in the majority of conventional convolutional networks by enabling neural networks to standardize unpredictable input data through spatial transformations. On computer vision tasks, this results in increased efficiency and accuracy.
Canonical Pose Normalization: To make it simpler to compare input objects for similarities or differences, STNs employ adaptive modification to create a canonical, standardized pose.
Reduced Error Rates: STN-containing models perform noticeably better than their traditional predecessors, resulting in a huge reduction in error rates, especially in noisy situations or with distorted data. For instance, on distorted MNIST datasets, ST-CNNs performed better than normal CNNs and FCNs.
Computational Efficiency: Because of future downsampling, the module may provide speedups in attentive models. It is computationally very quick and does not substantially slow down training speed.
Automatic Feature/Part Detection: As demonstrated in bird classification challenges where various transformers learnt to focus on particular parts like heads or bodies, STNs are capable of autonomously finding and learning part detectors in a data-driven way without the need for extra supervision.
Focus on Relevant Regions: They make it possible for networks to choose and convert the most pertinent areas of a picture to a canonical posture, which makes inference in later layers easier.
Challenges and Limitations
Complexity: STNs have the potential to complicate a model’s interpretation and comprehension.
Computational Cost: Despite STNs’ innate efficiency, training them can be costly and time-consuming.
Feature Map Alignment: Since STNs only carry out spatial changes, they may not always match the feature maps of a converted picture to those of the original in the majority of cases. This could result in a reduction in classification accuracy when converting CNN feature maps. Training deeper localization networks can be challenging.
Aliasing Effects: If sampling kernels with fixed, limited spatial support are employed, downsampling with a spatial transformer may result in aliasing effects.
Limited Parallel Objects: The maximum number of objects that a solely feed-forward network may model at once is determined by the number of parallel spatial transformers.
Technologies and Frameworks
For implementation, TensorFlow and PyTorch are the primary deep learning frameworks used for STNs.
- TensorFlow is renowned for its adaptability in creating custom layers, which is essential for putting the grid generator, sampler, and localisation network into practice.
- The dynamic computational graphs in PyTorch facilitate the intuitive coding of intricate transformation and sampling procedures. Affine_grid and grid_sample functions are among the built-in Spatial Transformer Network support capabilities.
Optimization and Best Practices
STNs need to be optimised for complicated use cases, particularly during training, even with effective architectures.
Loss Functions: It’s critical to choose suitable loss functions carefully. To avoid data distortion from STN transformations and guarantee useful output, transformation consistency loss and task-specific loss functions are usually combined.
Regularization Techniques: Several regularization strategies, such as dropout, L2 Regularization (weight decay), and early stopping, help prevent overfitting and enhance generalization.
Training Data: Enhancing the training data’s quantity, variety, and breadth is also essential for performance.
Real-World Applications and Case Studies
STNs have greatly advanced the science of computer vision by demonstrating their value in a wide range of real-world application cases:
- Image Classification and Object Detection: This is a primary application, where STNs improve the robustness of models to varying presentations of objects in datasets.
- MNIST Dataset: Despite a wide range of possible variances, STNs can significantly reduce mistake rates by centering and normalizing handwritten digits.
- Street View House Numbers (SVHN): By efficiently cutting and rescaling feature map segments that correspond to digits, STNs have achieved state-of-the-art results in multi-digit recognition, concentrating resolution and network capacity on these regions.
- Fine-Grained Classification (e.g., Bird Classification): STNs with multiple parallel transformers have shown state-of-the-art performance by automatically discovering and attending to object parts (e.g., head and body) without explicit keypoint training data.
- Visual Attention Modelling: STNs are more adaptable and trainable using pure backpropagation without reinforcement learning, making them suitable for applications requiring an attention mechanism.
- Data Augmentation: By creating modified versions of preexisting data, STNs can be utilized for data augmentation.
- Co-localization: An STN can locate distinct instances of an unknown class within a collection of photos.
- Healthcare: STNs improve the accuracy of medical imaging and diagnostic instruments, particularly for subtle variations in patients such as tumours. In hospital settings, they can also increase operational effectiveness and compliance.
- Autonomous Vehicles: Because STNs are computationally efficient and can handle dynamic and visually complex scenarios in real-time, they help with trajectory prediction for self-driving and driver-assist systems. Capabilities for temporal processing can further enhance performance.
- Robotics: Especially in intricate and novel contexts for object-handling tasks, STNs help to achieve more accurate object tracking and interaction. For instance, STNs were used by TransMOT (Spatial-Temporal Graph Transformer for Multiple Object Tracking) to enhance robot perception systems for manipulating and recognizing objects.
- Integration with Recurrent Neural Networks (RNNs): Studies combining STNs with RNNs have demonstrated encouraging outcomes in sequence prediction tasks, such as digit identification on crowded backdrops.
- Generative Adversarial Networks (GANs): By combining STNs with GANs, “ST-GANs” can enhance sequence prediction and image-generating capabilities.
- Data Lakehouse Environments: STNs can preprocess picture data in a data lakehouse, which improves input for machine learning algorithms and facilitates more effective data analysis, even if their primary use is in computer vision.
Relationship to Other Neural Network Ideas
STNs are connected to neural network concepts:
STNs are effective in recurrent models and can help disentangle object reference frames. Neural Turing Machines, which use external memory, are controlled by gated RNNs called LSTMs.
The topic of creating interpretable representations for transformations is addressed in Deep Convolutional Inverse Graphics Networks (DC-IGN) using an encoder-decoder model trained with Stochastic Gradient Variational Bayes (SGVB). Denoising autoencoders and generative stochastic networks (GSNs) can define and learn a manifold and train generative machines to take samples from a specified distribution.
Adversarial networks can construct a stochastic extension of deterministic MP-DBMs, known as Deep Boltzmann Machines (DBMs). Deep belief networks use Restricted Boltzmann Machines (RBMs) and greedy layer-wise unsupervised learning to create deep generative models.
ResNets use “shortcut connections” or “identity mappings” to smooth gradient flow in deep architectures, addressing vanishing/exploding gradient issues and enabling deeper model training. This approach to deep network training is unique.
Radial Basis Functions (RBFs): Ideal for high-dimensional interpolation, this multilayer network ensures a guaranteed learning algorithm by solving linear equations.
