In this article, we can learn what Deconvolutional Networks are, the architecture of DNs, history, Advantages, disadvantages of DNs, challenges, features, and types of DNs
A unique method in artificial intelligence for image processing tasks is represented by Deconvolutional Networks (DNs), also referred to as deconvolutional neural networks. In essence, they are reversible Convolutional Neural Networks (CNNs) that build images upward from processed input.
What is Deconvolutional network?
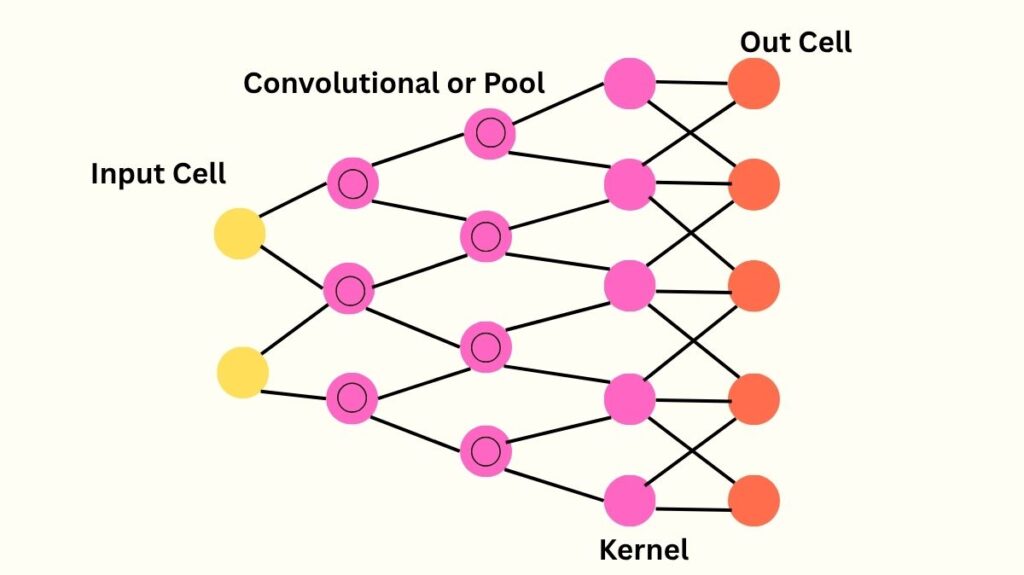
A deconvolutional network, also known as a transposed convolutional network, is a kind of neural network that upsamples feature maps and is frequently used to restore spatial dimensions that are lost during pooling or convolution. It is helpful for applications like image segmentation, super-resolution, and autoencoders since it “reverses” the convolution process. It learns to transfer low-resolution features back to higher-resolution outputs, in contrast to doing real deconvolution, as the name suggests.
The goal of deconvolutional networks is to retrieve lost signals or features that a conventional CNN might not have deemed significant. DNs are intended to produce a high-resolution (HR) image from a given low-resolution (LR) image in the context of Single Image Super-Resolution (SISR), a crucial application. Deconvolution is perfect for picture reconstruction, where information flows from “less to more” because it is made to extract more plentiful information from fewer features, in contrast to convolution, which is a process of information reduction.
History of DNs
The idea behind deconvolutional networks stems from the larger category of “deep learning” techniques that aim to identify hierarchical characteristics in data. While methods such as sparse auto-encoders and Deep Belief Networks (DBNs) similarly generate feature hierarchies in an unsupervised fashion, DNs are very different. One significant difference is that, instead of depending on encoders that might approximate these features, Deconvolutional Networks are decoder-only models that solve the inference issue directly to calculate latent representations. Embedding deconvolution procedures within multilayer feedforward neural networks was investigated in early studies.
Architecture of Deconvolutional network
- An input image with K0 color channels is fed into a single layer of a deconvolutional network.
- A linear sum of K1 latent feature maps (zik) convolved with learnt filters (fk,c) is used to represent each channel of the input picture.
- A regularisation term on zik is added to promote sparsity in the latent feature maps, creating an overall cost function, in order to produce a unique solution from an under-determined system.
- These layers are stacked to create a hierarchy, with layer l receiving its input from the feature maps of layer l-1. In contrast to certain other hierarchical models, DNs do not automatically carry out pooling, sub-sampling, or divisive normalization between layers, though these could be included.
- The cost function for layer l generalizes this concept, with glk,c being a fixed binary matrix that determines connectivity between feature maps at successive layers.
Mechanism of Deconvolutional network
Filters are learnt by alternating between minimising Cl(y) over the filters while maintaining feature maps fixed and minimizing the cost function (Cl(y)) over the feature maps (inference).
- Starting with the initial layer, this minimization is carried out layer by layer.
- To deal with poorly conditioned cost functions that appear in a convolutional situation, the optimization uses strong approaches.
- In order to reconstruct a picture, the model first breaks down an input image by utilizing the learnt filters to infer the latent representation (z). In order to project the feature maps back into the picture space, this procedure may need alternating minimization phases.
- Adding an additional feature map (z0) for each layer 1 input map and connecting it to the image using a constant uniform filter (f0) with a l2 prior on its gradients (||∇z0||2) is a crucial reconstruction detail. Learnt filters can simulate high-frequency edge structure by using these z0 maps, which capture low-frequency components.
Advantages and disadvantages of DNs
What are the Advantages of DNs?
Deconvolutional networks have a number of noteworthy advantages.
Better Performance with Less Complexity
Without requiring more intricate structures or deeper network depth, a fully deconvolutional network with just 10 layers can outperform deeper CNNs (20–30 layers) in Single Image Super-Resolution.
Ideal for Reconstruction
Because deconvolution procedures reverse the information loss that frequently happens in conventional convolution processes, they are naturally well-suited for image reconstruction. This is because they can recover and restore more detailed information from sparse features.
Unsupervised Feature Learning
DNs are highly skilled at building hierarchical image representations without the need for labelled training data. This enables them to naturally find rich, mid-level features like edge junctions, parallel lines, curves, and geometric aspects.
Advanced Activation and Loss Functions
Training stability is increased by utilising the Exponential Linear Unit (ELU) activation function, which helps to mitigate the “Dying ReLU” issue. By including Kullback-Leibler divergence in the loss function, the typical problem of over-smoothness in reconstructed pictures brought on by Mean Squared Error (MSE) is avoided.
Computational Efficiency
DNs have shown notable computational cost savings (e.g., up to 90% decrease in FLOPs) in certain applications, such as medical picture segmentation, while preserving or improving performance and successfully restoring high-frequency details.
Robust Feature Extraction
They generate a variety of filter sets that capture complex image structures without the need for extra CNN modules like pooling layers or intensive hyper-parameter tuning.
Whole-picture Processing
DNs process the full picture at once, in contrast to patch-based sparse decomposition techniques. This is essential for learning rich and robust features and produces more stable latent feature maps.
Also Read About Multilayer Perceptron History, How it works And Features
Disadvantages of DNs
Despite their clear benefits in feature learning and picture reconstruction, deconvolutional networks do have some disadvantages and things to keep in mind:
Complexity and Slowness of Computation:
- It can be computationally demanding to solve a multi-component deconvolution problem in order to infer feature map activations in a deconvolutional network.
- Learning these networks can be a very slow optimisation process that may take thousands of iterations to converge.
- While Iterative Reweighted Least Squares (IRLS) is too slow for large datasets, certain optimisation techniques, such as direct gradient descent, can result in “flat-lining” and subpar solutions. All things considered, the procedure may be slower than methods that use bottom-up encoders for inference.
The problem of ill-conditioned minimization
The fundamental method of the deconvolutional network is the inference of optimal feature maps, which might result in a poorly conditioned minimisation problem even when they are convex (for example, with an L1 sparsity term). This indicates that it is challenging to efficiently converge to a viable solution since the elements in the feature maps are significantly linked through the filters.
False Terminology
The deep learning community views the term “deconvolutional layer” as regrettable and deceptive. True mathematical deconvolution is not something it performs.
The terms “transposed convolutional layer” or “fractionally strided convolution” are more appropriate. In reality, “deconvolution” is a particular kind of convolution that translates feature maps to a higher-dimensional space, frequently incorporating padding and distinct stride logic. This can lead to confusion because the phrase implies an opposite operation, similar to how division is to multiplication.
Features and Capabilities
- The main application for creating high-resolution photographs is Single Image Super-Resolution (SISR).
- Image Analysis and Synthesis: Used for both producing and deciphering images.
- Hierarchical Feature Extraction: Able to learn and extract a wide range of intricate features, from mid-level concepts and higher-order image structures to low-level edges.
- Image denoising: This technique effectively lowers noise and enhances image quality.
- Object Recognition: Performs competitively with other approaches and can be used as effective feature extractors for object recognition applications.
- Medical picture Segmentation: Shown to be useful in specific domains, this technique has been successful in both 2D and 3D medical picture segmentation.
- Learnable Parameters: The network’s reconstruction parameters and filters are learnt to adjust to the data for best results.
Type of DNs
Although the name “Deconvolutional Networks” describes a broad class, certain sources point to particular implementations:
- Fully Deconvolutional Neural Networks (FDNNs): Using only deconvolutional layers, FDNNs are designed for SISR.
- Deconver: A specialised DN designed for medical image segmentation, it achieves great precision and efficiency by utilizing non-negative deconvolution (NDC) operations within a U-shaped architecture.
Challenges
- Computational Intensity: The multi-component deconvolution problem that must be solved in order to infer feature map activations can be computationally taxing.
- Ill-Posed Nature: SISR and other image reconstruction issues are frequently ill-posed, which means that a single low-resolution input may correspond to several alternative high-resolution images.
- Optimization Challenges: In a convolutional environment, training DNs entails minimising intricate and possibly poorly conditioned cost functions, which calls for strong optimization strategies.
- Terminology Confusion: Because the phrase “deconvolutional layer” refers to a “transposed convolution” operation a convolution with particular parameters that allow upsampling rather than a mathematical deconvolution (an inverse operation), it sometimes causes confusion.
Also Read About Gaussian Restricted Boltzmann Machine And Binary RBM
Distinctions from alternative models
CNNs or convolutional networks: Although they function differently, Deconvolutional network and CNNs share a similar ethos. CNNs process input signals using a “bottom-up” methodology that involves several layers of convolutions, non-linearities, and sub-sampling. On the other hand, every layer in a deconvolutional network is “top-down” and seeks to produce the input signal by adding together feature map convolutions using learnt filters.
Sparse Auto-Encoders and Deep Belief Networks (DBNs): Similar to DNs, these models build layers from the image upwards in an unsupervised manner out of greed. Usually, they are composed of a decoder that maps latent features back to input space and an encoder that maps to latent space from the bottom up. However, DNs do not have an explicit encoder; instead, effective optimization approaches are used to directly address the inference problem, which involves identifying feature map activations. This could result in better features since it enables DNs to calculate features precisely rather than roughly. Another restriction on DBN building blocks, known as restricted Boltzmann machines (RBMs), is that the encoder and decoder must share weights.
Patch-based Sparse Decomposition: DNs are not the same as methods that use tiny picture patches for sparse decomposition (e.g., Mairal et al.). DNs carry do sparse decomposition throughout the entire image simultaneously, which is thought to be essential for effectively learning rich features. When patch-based techniques are stacked, they may result in higher-layer filters that are just bigger versions of the first layer filters and do not have the varied edge compositions that are present in the upper layers of DNs. Additionally, when layers are stacked, patch-based representations may be extremely unstable across edges, making it difficult to learn higher-order filters.
Performance and Experiments of Deconvolutional network
DNs were trained on 100×100 datasets of urban settings and natural scenes (fruits and vegetables), showing how multi-layer deconvolutional filters develop on their own.
Object Recognition (Caltech-101): DNs showed competitive performance in object recognition, marginally surpassing SIFT-based algorithms and other multi-stage convolutional feature-learning techniques such as feed-forward CNNs and convolutional DBNs. Concatenating the spatial pyramids of both layers prior to constructing SVM histogram intersection kernels produced the best results.
Denoising: It was demonstrated that a two-layer DN model could efficiently denoise photos by drastically lowering Gaussian noise. For example, the first layer lowered the noise at 13.84dB to 16.31dB, and the second layer’s reconstruction further reduced it to 18.01dB.
