Feed Forward Neural Network Definition
A basic kind of neural network design, FFNNs are identified by their layered structure and the direction of information flow. They are extensively utilised, especially in applications involving natural language processing.
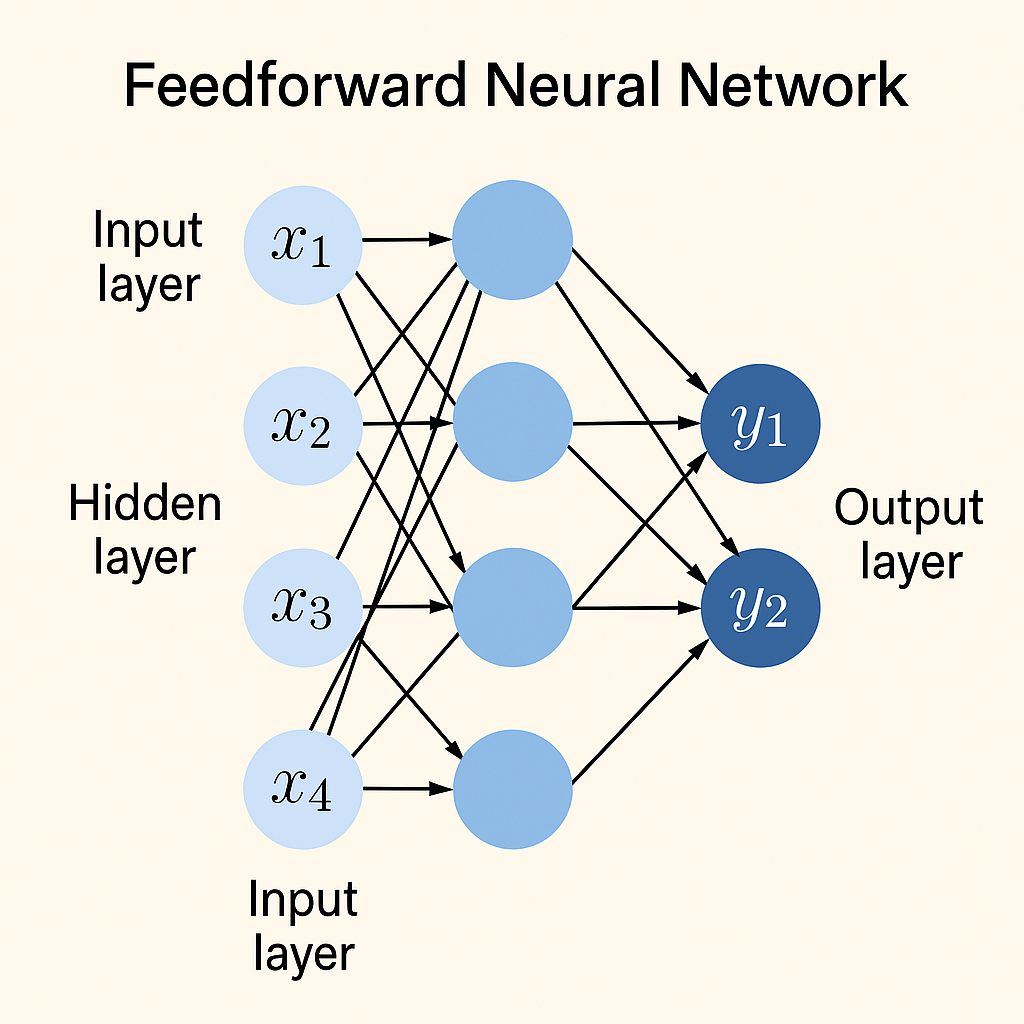
- Neural networks with units connected without cycles are called feed-forward networks.
- Data moves from the input layer to the output layer via any hidden layers in a single direction. Each layer’s units transfer their outputs to the units in the layer above it; no outputs are returned to the lower layers.
- An input layer, one or more hidden layers, and an output layer are usually their three primary parts. Numerical data representations or raw feature values are fed into the input layer. The layers in between the input and the output are known as hidden layers. For the classes or goal values that need to be learnt, the output layer generates scores.
- A fully-connected network, in which every neurone in a layer is connected to every other neurone in the layer above, is a typical configuration. Weights relate to the relationships between layers.
Computation and Function
- A neural network’s fundamental unit is a single computational unit called a neurone. Every unit calculates an output after receiving a collection of real-valued numbers as input.
- A non-linear activation function is applied after each input has been multiplied by its weight, added to the sum, and a bias term has been added. Important are the non-linear activation functions. A multi-layer network would reduce to a linear transformation basically, a linear classifier in their absence.
- The Rectified Linear Unit (ReLU), sigmoid, and tanh are examples of common non-linear activation functions. In general, ReLU and Tanh outperform Sigmoid. To generate a probability distribution across classes, the output layer may employ a softmax function for multi-class classification.
- Vector-matrix operations can be used to efficiently represent and carry out the computations. The term “layer” is frequently used to describe the vector that emerges following a linear transformation.
You can also read Bidirectional LSTM vs LSTM Key Differences Explained
Terminology
- Multi-layer feed-forward networks are sometimes called Multi-layer Perceptrons (MLPs) for historical reasons. In contrast to the solely linear perceptron, contemporary networks employ non-linear units, therefore this is technically a misnomer.
- They can also be seen of as a computational graph, in which a composition of functions calculated at each node is optimised in order to learn the parameters (weights and biases).
Relationship to Perceptrons and Linear Models
- FFNNs are thought of as a generalisation of logistic regression and perceptrons.
- With only one input layer and one output node, the perceptron is referred to as the most basic neural network.
- Feed-forward networks can tackle issues like the XOR problem that linear models are unable to handle by incorporating hidden layers.
Theoretical Power and Deep Learning
- Theoretically, feed-forward networks with hidden layers can represent any Borel-measurable function, making them a powerful hypothesis class known as universal approximators.
- In practice, though, this universal approximation capability might necessitate a very high number of hidden units.
- Deep networks are networks that have multiple hidden levels. Because modern neural nets are often deep, the utilisation of these networks is commonly referred to as deep learning. In contrast to very wide shallow networks, deeper networks can occasionally simulate more complex functions with fewer parameters.
Training
- Stochastic gradient descent and other gradient-based optimisation methods are used to train FFNNs.
- Backpropagation, which effectively calculates a loss function’s gradients with respect to all network parameters, is the main algorithm utilised. Backpropagation makes use of dynamic programming and the calculus chain rule.
- Learning parameters (weights and biases) that minimise a selected loss function according to the discrepancy between the network’s output and the actual target values in the training data is the aim of training.
Representation Learning and Feature Engineering
- The capacity of early layers of neural networks, particularly FFNNs, to learn abstract representations of the input data that are helpful for subsequent layers is one of their strengths.
- They can operate on inputs of a fixed size or variable length, such as documents that are represented as a bag of words, where the elements’ order may be ignored.
- For inputs like words, they frequently employ dense vector representations, or embeddings, which can be learnt during training or pre-trained.
- FFNNs eliminate the need for manual feature engineering, which was prevalent in previous linear models, by automatically learning useful feature combinations.
Applications in NLP and Beyond
- FFNNs can be applied to a number of NLP tasks, such as structured prediction, language modelling (predicting the next word), classification (such as sentiment analysis), and language understanding tasks.
- They can also be applied to autoencoder designs for dimensionality reduction.
- Convolutional neural networks (CNNs), recurrent neural networks (RNNs), transformer networks, encoder-decoder models, and other more intricate neural network topologies sometimes use FFNNs as parts or layers. Transformer networks, for example, employ position-wise feed-forward layers subsequent to self-attention levels.
Feed Forward Neural Network Architecture
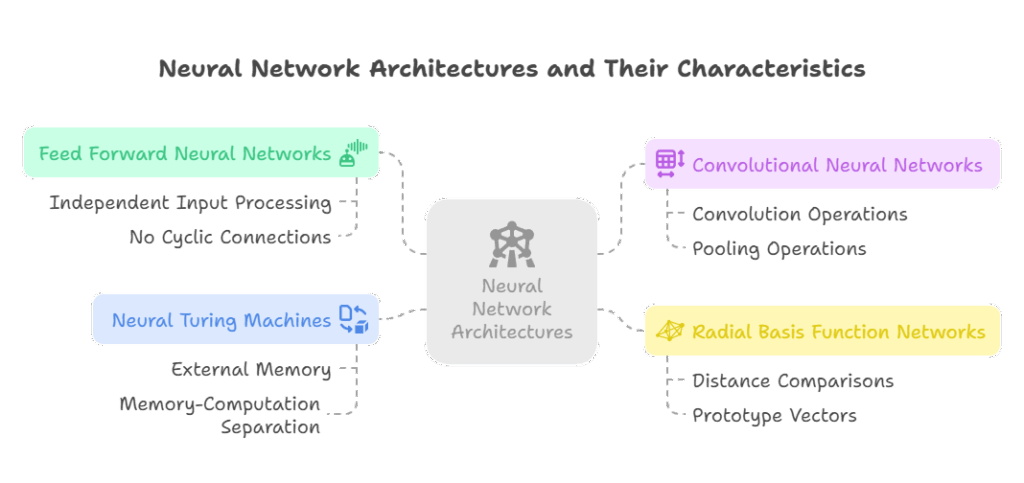
- FFNNs process inputs independently or disregarding order, and they do not have the cyclic connections found in Recurrent Neural Networks (RNNs), which are intended for sequential data and have cycles to retain state over time.
- Specialised feed-forward architectures known as Convolutional Neural Networks (CNNs) are excellent at processing grid-like input, such as photographs, and employing convolution and pooling operations to find local patterns.
- An unsupervised hidden layer based on distance comparisons to prototype vectors is a characteristic of Radial Basis Function (RBF) networks.
- Compared to conventional FFNNs or RNNs, Neural Turing Machines (NTMs) offer a more distinct division between memory and computation by supplementing neural networks (often RNNs) with external, accessible memory.
Recent Advancements:
By detecting and parallelizing sequences of FFN layers, a new method known as FFN Fusion optimises huge language models while maintaining performance. This results in lower inference latency and cost.
In conclusion, feed-forward neural networks are basic layered neural architectures that use backpropagation to train weighted connections and activation functions to learn intricate, non-linear interactions. They serve as the foundation for many neural network concepts and are frequently incorporated as parts of more intricate models, while being less sophisticated than certain contemporary architectures like RNNs or Transformers.
You can also read An Introduction To Latent Semantic Analysis LSA In NLP
