An Introduction To Latent Semantic Analysis
Latent Semantic Analysis (LSA), sometimes known as LSI, is a Natural Language Processing approach used in text categorization and information retrieval. One of the oldest methods for word embeddings or representations.
The Distributional Hypothesis, which postulates that words that occur in comparable settings often have similar meanings, is the underlying theory of LSA. The classic quote “you shall know a word by the company it keeps” by J.R. Firth encapsulated this notion. By examining the word distribution in extensive text corpora, LSA aims to quantify this concept.
key aspects of Latent Semantic Analysis
The following summarizes the main features of LSA:
Input Data: The first step in Latent Semantic Analysis is creating a word-context matrix, which is frequently a term-document matrix. Words (or terms) are represented by rows in this matrix, while contexts (such as documents or windows of surrounding words) are represented by columns. The matrix’s entries, which are usually based on co-occurrence counts, measure how strongly a word and a context are associated. For instance, logarithmic scaling and division by document frequency or Pointwise Mutual Information (PMI) might be used to weight or normalize these numbers. The raw matrix is frequently high-dimensional and sparse.
Mathematical Core: The Latent Semantic Analysis relies heavily on Singular Value Decomposition (SVD), which is a mathematical approach. SVD is a technique for reducing dimensionality. To represent the data in a lower-dimensional domain, it breaks down the high-dimensional word-context matrix. To determine the dimensions along which the data fluctuates the most, SVD is applied to the matrix. In a least-squares sense, this projection into the lower-dimensional space is selected ideally to maintain the most significant linkages.
Latent Semantic Space: “Latent” semantic dimensions are the dimensions in the reduced space. The original dimensions have been combined linearly. The premise is that this latent space reflects an underlying semantic structure or “true representation” that may be hidden by differences in language usage between documents in the original high-dimensional space. Even if they don’t always appear together, words that regularly co-occur in the original data are projected onto comparable dimensions in this latent space, which raises their similarity score.
Output: Dense Vectors/Embeddings: Each word is represented by a dense vector in this lower-dimensional space as a result of applying SVD while maintaining the upper k dimensions. The majority of the values in these dense vectors are not zero, in contrast to the initial sparse vectors. The mapping from the sparse count vector space to the dense latent vector space is where the word “embedding” first appeared in this context. Semantic information is what these vectors are meant to capture.
Semantic Similarity: By calculating the distance or angle between the respective vectors of words or texts in the latent semantic space often using the cosine similarity the semantic similarity between them may be quantified. Vectors for words or documents with similar meanings should be next to one another.
Latent Semantic Analysis Example
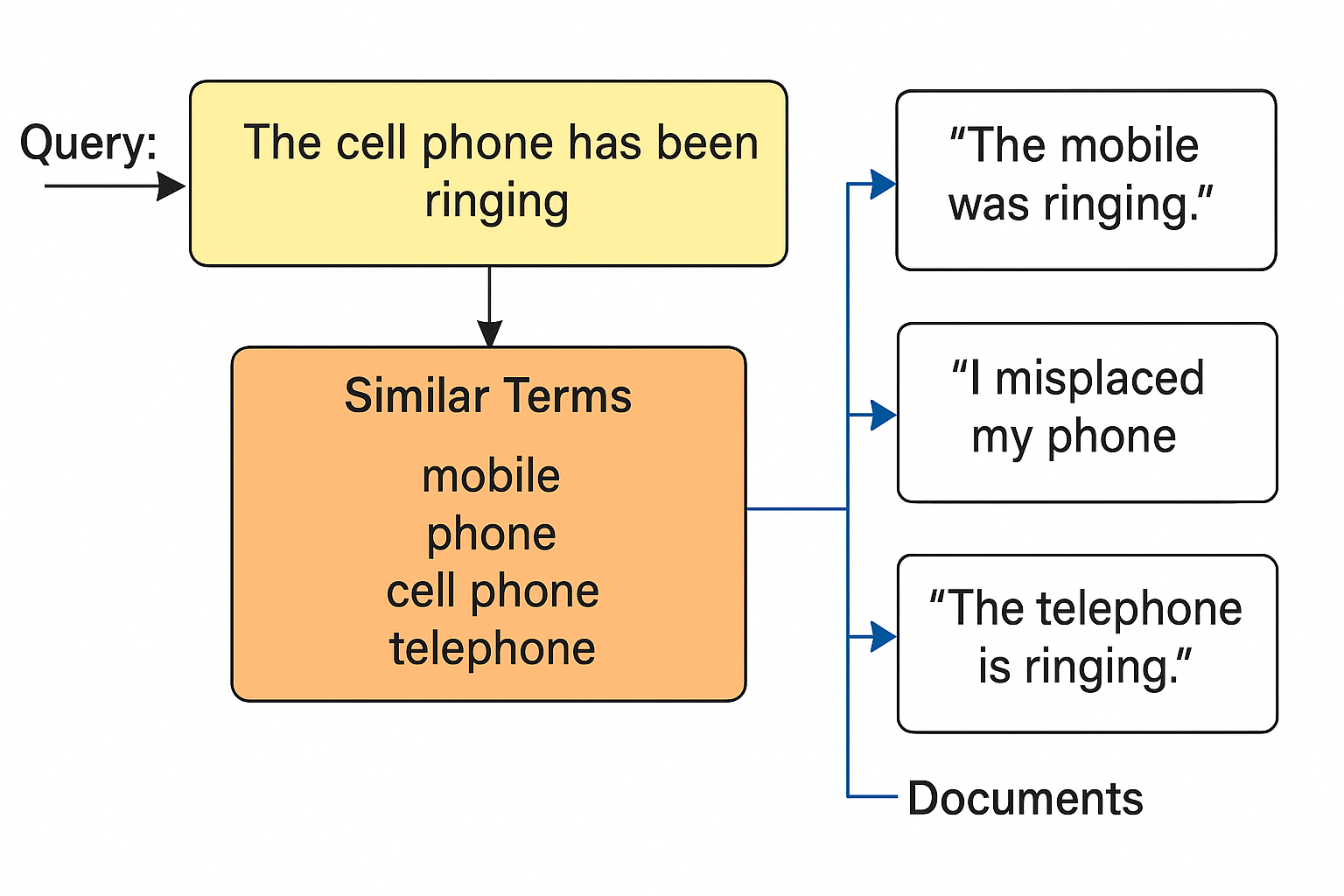
mobile, phone, cell phone, telephone are all similar but if we pose a query like “The cell phone has been ringing” then the documents which have “cell phone” are only retrieved whereas the documents containing the mobile, phone, telephone are not retrieved.
Applications
LSA has been effectively used for a number of purposes, such as:
- By matching document vectors to query vectors, information may be retrieved.
- Text Categorisation.
- Calculating the semantic similarity of words.
- Examining how semantics evolve throughout time.
- Initial efforts in essay grading, multiword expression identification, and morphology induction.
- As characteristics for Named Entity Recognition and other NLP tasks.
Limitations
The basic Latent Semantic Analysis model’s ability to generate context-independent word representations is a noteworthy feature. Regardless matter whether the term “bank” refers to a riverbank or a financial organization, it receives a single vector. This restricts its capacity to deal with polysemy, or words that have more than one meaning. The latent space’s dimensions are determined theoretically and could be difficult for people to understand. Additionally, biases in the training corpus may be reflected in LSA.
Many later distributed and dense vector representation techniques in NLP were made possible by Latent Semantic Analysis. It shown that using only word co-occurrence data, significant semantic information could be gleaned from unprocessed text.
Probabilistic Latent Semantic Analysis (PLSA)
key points about PLSA
The following are the salient features of PLSA:
Early Topic Model: PLSA is considered to be among the first topic models. To find themes in a corpus and give each document a probability distribution, topic modelling approaches such as PLSA, Latent Dirichlet Allocation (LDA), and Non-negative Matrix Factorisation (NMF) are employed.
Distinction from SVD-based LSA: The underlying mathematical limitations of PLSA are different from those of normal LSA (or LSI), which factors a word and context count matrix using Singular Value Decomposition (SVD) to produce continuous vector representations of words. The basis vectors in PLSA, which may be viewed as underlying factors or themes, are not orthogonal. Furthermore, the modified representations (such as document representations in terms of themes) and the basis vectors in PLSA are both required to have non-negative values.
Relationship to Non-negative Matrix Factorization (NMF): The connection between NMF and PLSA. PLSA is equivalent to the first topic models in the context of Restricted Boltzmann Machines (RBMs) for topic modelling. They also point out that, in contrast to SVD-based LSA, PLSA’s basis vectors are not orthogonal and that both basis vectors and transformed representations are non-negative, which is also true for NMF.
Semantic Usefulness of Non-negativity: Since the non-negative value of each converted feature can indicate the intensity of a subject in a given text, the non-negativity requirement in models such as NMF (and by extension, PLSA) is semantically valuable.
To put it simply, PLSA is a probabilistic method for identifying latent structure in text that is comparable to LSA but uses distinct mathematical restrictions (non-negativity and non-orthogonality) and is associated with the topic model family and NMF, while conventional LSA depends on SVD.
