What is ECDLP?
Elliptic Curve Cryptography (ECC), a public key cryptography, uses the Elliptic Curve Discrete Logarithm Problem to secure its security. Its computational difficulty makes it suitable for cryptography.
The main features of Elliptic Curve Discrete Logarithm are as follows:
- The primary distinction between Elliptic Curve Discrete Logarithm and conventional discrete logarithm problems (DLP) is found in the mathematical structure that underlies each of them.
- Elliptic curves, which are described by polynomial equations like y² = x³ + ax + b, over finite fields, are the basis of ECDLP. The secp256k1 curve, for instance, is used by Bitcoin and has the formula y² = x³ + 7.
- The arithmetic of finite fields is the foundation of traditional DLP.
Operations and Definition of the Problem The Elliptic Curve Discrete Logarithm has the following definition when referring to elliptic curves:
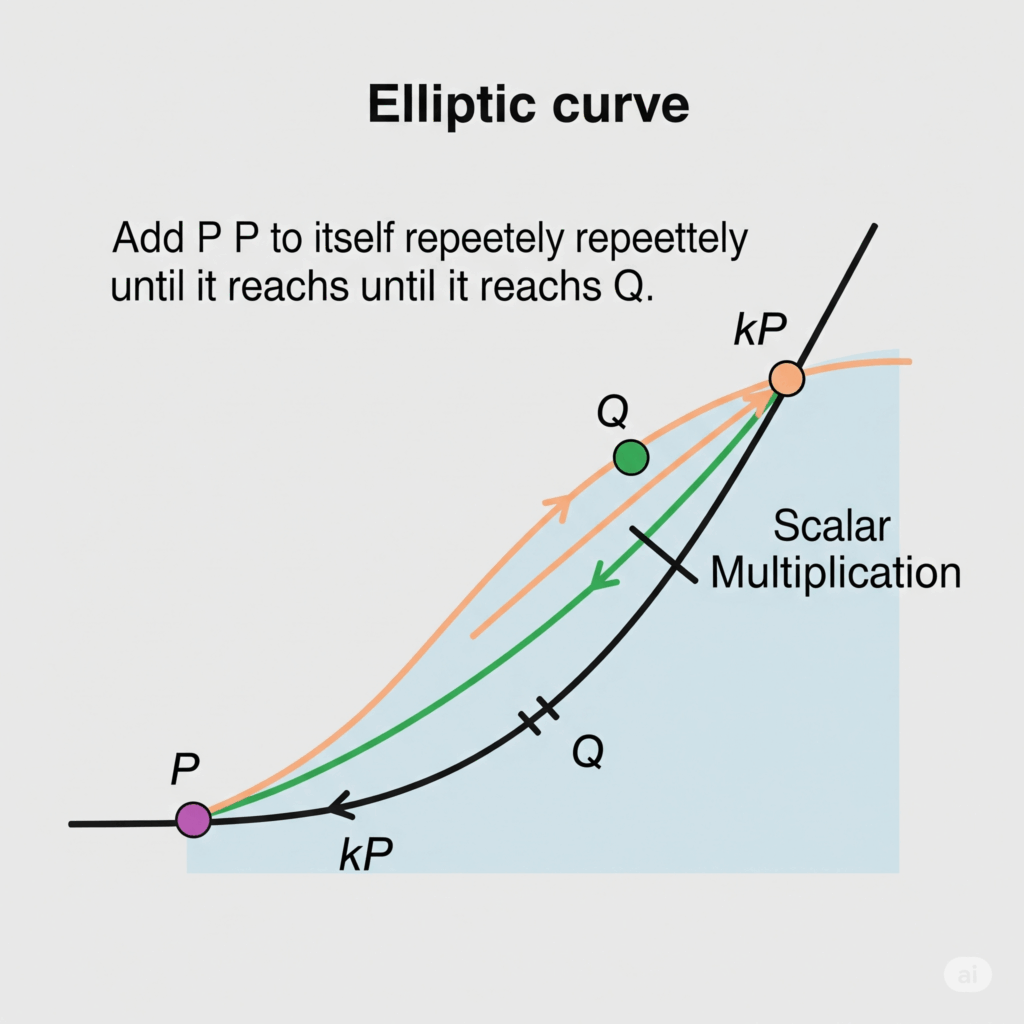
Given an elliptic curve E over a finite field, a point P on E, and another point Q on E, the problem is to find an integer k (if it exists) such that Q = kP. In this case, the goal is to find the scalar k, while P and Q are known. In essence, scalar multiplication is a repeating point addition on the elliptic curve, and this kP operation expresses it.
The fundamental group operations used in ECC and Elliptic Curve Discrete Logarithm are point doubling, which involves drawing a tangent line through a single point on the curve, and point addition, which involves drawing a line through two points on the curve to obtain a third intersection point. ECDLP, to put it simply, is the process of calculating the number of times you added P to itself in order to achieve Q, given the beginning point P and the final position Q after adding P to itself several times.
Computational Difficulty (Intractability)
There is currently no effective algorithm for determining k given P and Q, making the ECDLP a computationally challenging problem to tackle. ECC’s security is guaranteed by this challenge. Reversing the scalar multiplication operation is computationally impossible, which makes ECDLP intractable. It is quite hard to get d given P and T, yet it is simple to compute T from d and P (where T = dP). A “one-way function” is what this characteristic makes it. The index calculus method and the number field sieve are two more efficient methods that can be used to solve the classical discrete logarithm problem in finite fields, but no such algorithms are known for ECDLP.
Trying every value of k until the equation is fulfilled is the generic brute force strategy, which is the most well-known method for solving ECDLP. This method is computationally unfeasible for elliptic curves with sufficiently big parameters and large prime fields, though, as the number of possible possibilities for k increases exponentially with field size. For example, there are roughly 2256 potential values for k if a prime field is of order 256 bits. This means that a brute-force assault would require “astronomical amounts of time and computational resources” that are beyond the capabilities of present technology.
Security Implications and Applications
The premise that it is computationally impossible to solve the ECDLP is the only basis for the security of ECC. All ECC-based cryptography systems would be compromised if an effective solution were found. ECDLP, which is difficult, lets ECC attain RSA-like security with reduced key sizes. Similar security exists with 3072-bit RSA and 256-bit ECC keys.
Smaller key sizes minimize computing overhead, accelerating operation and energy utilization. ECC/ECDLP efficiency benefits secure web connections (TLS/SSL) and resource-constrained devices like smartphones, smart cards, Internet of Things devices, and mobile phones.
Electronic signatures, encryption, and key agreement protocols employ ECC and ECDLP extensively. They serve as the foundation for the security of blockchain systems such as Ethereum and Bitcoin, for instance, where public keys are generated by multiplying a private key d (the integer represented by ECDLP) by a publicly known generating point P.
What is ECC’s foundation?
Elliptic Curve Discrete Logarithm Problem (ECDLP) is the starting point for Elliptic Curve Cryptography (ECC). The security of the public-key cryptography known as ECC is based on this mathematical problem. Specifically,
- ECC’s security depends on the presumption that it is computationally impossible to solve the ECDLP. Should an effective solution to ECDLP be found, it would jeopardize the security of all ECC-based cryptographic systems.
- ECC makes use of the assumed difficulty of ECDLP to develop secure cryptography solutions.
- The elliptic curve arithmetic over finite fields is the foundation of ECC. Equations using polynomials, like y² = x³ + ax + b, define these curves. For example, Bitcoin uses the secp256k1 curve y² = x³ + 7.
- Point addition, point doubling, and scalar multiplication make up the ECDLP. At the heart of the issue is scalar multiplication, which turns a point P into another point T by multiplying it by an integer d (dP = T). The challenge is to reverse this process, which is to find d given P and T.
Where is ECDLP primarily used?
In mathematics, Elliptic Curve Cryptography (ECC) is based on the Elliptic Curve Discrete Logarithm Problem (ECDLP). ECC, and consequently ECDLP, are widely utilized in a range of cryptographic applications where high performance or limited computational resources are necessary because to their effectiveness and robust security.
The main areas where ECDLP is utilised by ECC are as follows:
General Cryptographic Applications: Cryptographic applications such as digital signatures, encryption, and key negotiation protocols all require ECC.
Mobile and Wireless Devices: Since it works well, it is frequently found in wireless and mobile devices. IoT gadgets and smartphones are included in this. Smart cards and mobile phones with limited resources can benefit from ECC’s smaller key sizes, which reduce computational overhead, processing time, and energy usage.
Secure Web Communications: The role that ECC plays in secure web connections (TLS/SSL) is supported by ECDLP.
Blockchain Technologies: Blockchain platforms like Bitcoin and Ethereum make extensive use of ECC. Here, point T a random multiple of a generator point P that is known to the public is the public key, and the integer d is the private key. Within these networks, this is essential for money security and transaction verification.
What is the goal of ECDLP?
The Elliptic Curve Discrete Logarithm Problem (ECDLP) is a problem in which two known locations on an elliptic curve are related by an integer, usually represented by the letters “k” or “d.”
The difficulty is more precisely described as follows:
- Given an elliptic curve E over a finite field, a point P (or G as a generator) on E, and another point Q (or T or P) on E, the ECDLP aims to find the integer k (or d), if it exists, such that Q = kP.
- Finding the scalar k (or d) is the goal of this equation, where P (or G) and Q (or T or the other P) are known locations on the curve.
- Figuring out “how many times you added the starting point to itself to reach the ending point” is one way to conceptualize it.
Elliptic Curve Cryptography’s (ECC) security is based on a basic mathematical problem called the ECDLP. It is useful in cryptography because it is thought to be computationally difficult to solve, meaning that no effective solution exists for finding k given P and Q. Because of this, it is a “one-way function” quite straightforward to calculate Q from k and P, but quite challenging to obtain k given P and Q.
