In this article, we learn about the Schnorr signature, core concept, how it works, Schnorr Signature Example, Benefits, and Applications.
Schnorr signature
When the Schnorr signature algorithm is used, a digital signature is created. This digital signature system is well-known for being quick, easy, and producing brief signatures. In 1988, Claus Schnorr proposed it, and its patent expired in 2008, the year that Bitcoin was created. However, it wasn’t initially selected for Bitcoin because of its lack of testing and popularity.
Core Concept and Mathematical Basis
The mathematical characteristics of elliptic curves and discrete logarithms serve as the foundation for Schnorr signatures. They guarantee that a message hasn’t been altered and enable one side to demonstrate a private key’s ownership without disclosing it. It is among the protocols used to implement “Proof Of Knowledge,” an interactive proof in which a prover persuades a verifier that they are aware of something ‘X’ without explicitly disclosing ‘X’. With regard to Zero-Knowledge Proof, Schnorr signatures can be used.
How Schnorr Signatures Work
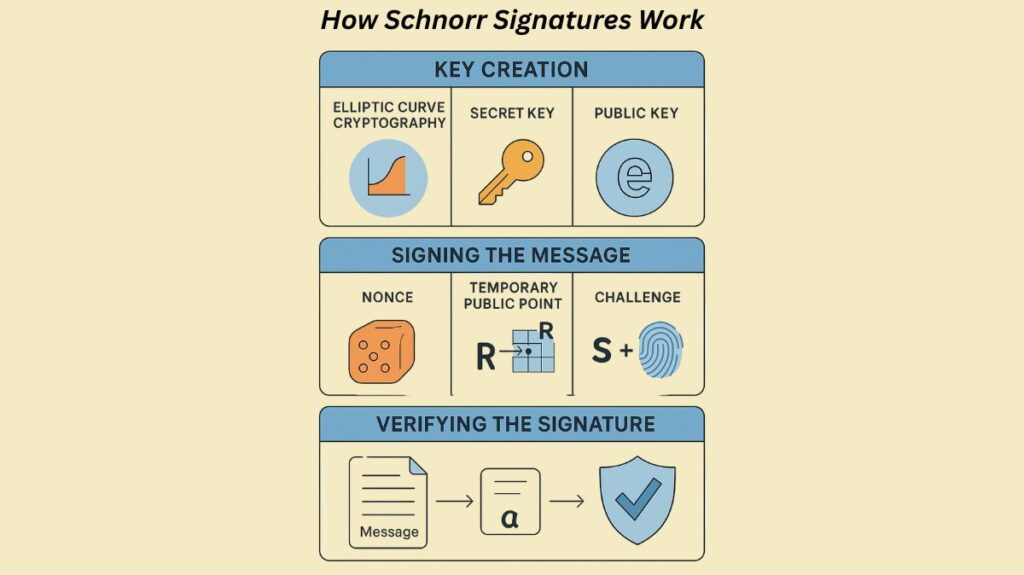
Key creation, message signing, and signature verification are all steps in the process. It is based on private-public key pairs and use elliptic curve cryptography, much like ECDSA. The main distinction is in the methods used for verification and signing.
Consider wanting to sign a communication to verify that it was sent by you:
Setting Up (Like getting your special pen and paper):
- Everyone uses “elliptic curve cryptography,” which is simply a fancy way of conducting arithmetic using curves and points, to comply with certain public math norms.
- Like a secret password, your secret key is a large, random number that only you know.
- You also have a public key, which is generated using the unique mathematical rules from your secret key. Anyone can have access to your public key.
Signing the Message (Putting your unique stamp on it):
- A “nonce” is a temporary secret number that you choose beforehand. One extremely crucial requirement is that it must be unique each time you sign something. Using the same one again could reveal your secret key!
- You generate a temporary public “point” (let’s call it ‘R’) by performing some calculations using the public math rules and your temporary secret integer.
- You combine the message you wish to sign with this short-term public point ‘R’. After that, you run this collection of data via a unique “hashing machine” a one-way mathematical process. ‘e’ is the brief, distinct “challenge” number that this machine puts out. ‘e’ can be thought of as a special fingerprint of your message and your transitory point.
- In the end, you perform a little more maths with the “challenge” number ‘e’, your original secret key, and your temporary secret number. ‘s’, the second element of your signature, is created in this way.
- Your entire signature consists of the’s’ number and the ‘R’ point, which is essentially just its X-coordinate. Together with your message, you send these two components.
Verifying the Signature (Checking if the stamp is real):
- Because you disclosed it, the person who gets your message and signature is already aware of your public key.
- They replicate the “challenge” number ‘e’, precisely like you did, using the message and the ‘R’ portion of your signature.
- Next, they use your public key, the “challenge” number ‘e’, and the’s’ portion of your signature to perform certain calculations.
- The signature is legitimate if the ‘R’ point they arrive at (more precisely, the ‘R’ X-coordinate) is the same as the one you first came up with!
Why is this cool?
You never reveal your secret key: Public data and the signature components are the only things used in the verification procedure. The signature cannot be used to determine your secret key due to the maths.
It’s efficient: Comparing this signature type to other others, the maths is quicker and easier.
Great for “group” signatures: This one is significant! Together, several persons can produce a singular signature that embodies each of them. It’s really helpful for:
- Saving space: It implies that transactions with a large number of signers are quicker and less expensive on blockchains since they use less space.
- Better privacy: Others find it more difficult to determine the number of participants since it makes multi-person transactions appear to be identical to single-person transactions.
It’s “non-malleable”: When someone else creates a Schnorr signature, it is extremely difficult to make minor changes and yet have the signature be accepted for the same message. This keeps some types of cunning attacks at bay.
Schnorr signatures are a secure, efficient, and cutting-edge way to digitally sign documents. They benefit systems like bitcoins that need security, efficiency, and anonymity.
You can also read What is Mempool in Blockchain, Purpose, and Implications
Zero-Knowledge Proof Properties
In order to demonstrate the three characteristics of zero-knowledge proof, the Schnorr protocol uses the example of Sanchita demonstrating her honesty to Sachin without disclosing her private key:
Completeness: Sachin believes Sanchita is honest because the calculated values are the same (X = X’, for example).
Soundness: Since Sanchita’s private key is the sole way to demonstrate her honesty, the proof is reliable.
Zero Knowledge: Sachin never finds out what Sanchita’s secret key is.
Key Properties and Benefits
Especially for blockchain applications, Schnorr signatures have a number of benefits over more antiquated systems like ECDSA.
Simplicity and Efficiency: There are fewer calculations, quicker verification times, and more effective implementations due to the simplified signature and verification methods.
Non-Malleability: Even if the key and message are the identical, a third party cannot alter a legitimate signature to create a different one. This stops some of the common threats in cryptocurrency applications, such making changes to a transaction signature to change the money or the people who receive it.
Linearity and Signature Aggregation: Combining several Schnorr signatures into a single, compact signature is made possible by this potent feature.
- Reduced Transaction Size and Fees: Aggregation lowers transaction fees, saves space, and lessens data load in blockchains, particularly for multi-signature transactions.
- Enhanced Privacy: In n-of-m configurations, aggregating signatures can create the illusion that multi-signature transactions are identical to single-signature transactions, hiding the number of signers and making it more difficult for observers to distinguish between single-sig and multi-sig expenditures or identify which participants signed.
- Batch Verification: Network processing is accelerated by the ability to validate several aggregated signatures more quickly than it is to check each one separately.
- Key Aggregation: Combining several public keys into a single “master” public key improves efficiency and privacy for interactions between multiple parties.
- Enhanced Security: Digital Signature Algorithm (DSA), Elliptic Curve Digital Signature Algorithm (ECDSA), and Edwards-curve Digital Signature Algorithm (EdDSA) are said to be slower and less secure than Schnorr. Additionally, they are provably secure based on accepted cryptographic assumptions.
- Shorter Keys: Shorter keys can be produced by Schnorr signatures.
Applications and Comparisons
Bitcoin: Bitcoin has used ECDSA, however there is a “movement to switch to a new approach that improves Bitcoin’s scalability, privacy, storage, and security.” Bitcoin’s 2021 Taproot upgrade (BIP-340) included Schnorr signatures, improving privacy, scalability, and flexibility for smart contracts and multi-signatures. Block 709,632 upgraded on November 14, 2021. Schnorr speeds up, secures, and simplifies the processing of digital signatures for Bitcoin. It is also backward-compatible, enabling a soft fork upgrade.
Byzcoin: The Schnorr signature is used by collective signing (CoSi), which is the foundation of the Byzcoin protocol, which is intended to safely scale blockchains using Byzantine consensus.
ECDSA vs. Schnorr:
- Based on elliptic curve cryptography, ECDSA was the current signature system in use in Bitcoin prior to Taproot. However, it lacked effective compression and joint signature verification.
- The length of a 256-bit ECDSA signature is twice that of the private key, or 512 bits. On the other hand, Schnorr signatures can combine several signatures into a single one because of their linearity, which effectively reduces the amount of the total data.
- Comparing Schnorr to ECDSA, the former offers reduced signature sizes, quicker verification times, enhanced defence against specific attack types, and signature aggregation capabilities.
- ECDSA is still a popular and secure signature technique, although Schnorr is frequently thought to be a better fit for Bitcoin. The decision is based on particular use cases and security needs.
- A wider range of digital signatures, such as RSA, ElGamal, DSA, ECDSA, EdDSA, blind signatures, multisignatures, threshold signatures, aggregate signatures, and ring signatures, are included in the Schnorr signature category.
Schnorr signature example

Without Schnorr:
Alice, Bob, and Carol need to sign → 3 separate signatures → more data → obvious that it was a multi-sig.
With Schnorr:
Alice, Bob, and Carol combine their keys and signatures → 1 single signature → smaller and private.
Summary Table
| Feature | ECDSA (Old) | Schnorr (New) |
| Signature size | Larger | Smaller |
| Verification speed | Slower | Faster |
| Multi-signature support | Multiple signatures | Single aggregated sig. |
| Privacy | Multi-sig is obvious | Looks like single-sig |
| Scalability | Less efficient | More efficient |
You can also read Merkelized Abstract Syntax Trees MAST Blockchain Benefits
