One of the most used unsupervised data analysis algorithms is K-Means clustering. Data points are clustered by similarity using this approach. K-Means is used in unsupervised learning, where data has no labels or outcomes. Its simplicity, intuitiveness, and efficacy have made the algorithm popular across many domains.
We’ll explain K-Means clustering’s benefits, drawbacks, and implementation in this article. We’ll also cover its machine learning and data science uses.
What is Clustering?
A machine learning technique called clustering groups related data elements. Grouping data into clusters that are more similar than others is the goal of clustering. Exploratory data analysis uses clustering to find hidden patterns, structures, and trends.
Machine learning algorithms identify organization in unlabeled data in unsupervised learning. Clustering helps when data patterns or categories are unknown.
K-Means Overview
The partition-based technique K-Means clustering separates data into a set number of clusters. Specify the number of clusters (k) before starting the algorithm. K-Means iteratively maps data points to clusters and refines them until they stabilize.
A K-Means algorithm assigns data points to clusters and updates cluster centroids. The algorithm improves its cluster comprehension and finds a solution over time.
How K-Means Works?
The iterative algorithm K-Means alternates between assignment and updating. The algorithm converges when cluster assignments don’t change after repeating these stages.
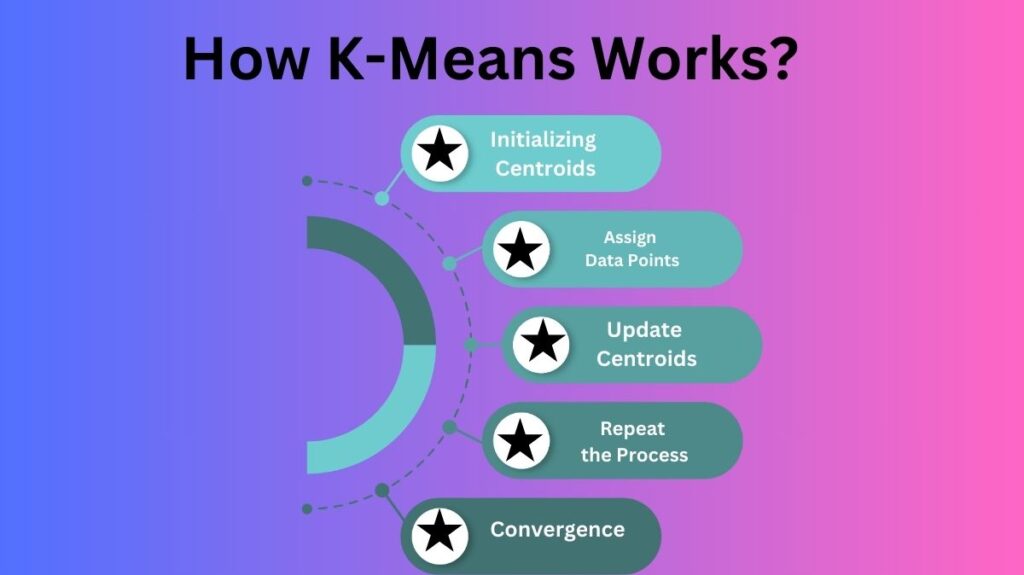
- Initializing Centroids: To create clusters, the algorithm randomly selects k data points as the starting centroids. Centroids are used to cluster data points by representing their “center”.
- Assign Data Points to the Nearest Centroid: Each dataset point is assigned to the nearest centroid when centroids are initialized. Similarity metrics, such as Euclidean distance, determine the assignment. Each data point is assigned to the cluster with the closest centroid, thereby clustering them.
- Update Centroids: After clustering all data points, centroids are updated. Each cluster’s new centroid is the mean of its data points. This assures that the centroid is the cluster’s “center” of data points.
- Repeat the Process: The algorithm repeats cluster assignment after updating centroids. Each data point is moved to the cluster with the closest centroid. The algorithm repeats the assignment and update phases until the centroids stop changing or a preset number of iterations is reached.
- Convergence: K-Means converges when centroids stabilize: data point assignments to clusters remain constant. Currently, the algorithm has categorized data into k clusters.
Determining the Number of Clusters (K)
Choosing the optimal number of clusters (𝐾) is a major difficulty in K-Means clustering. While the procedure requires a predetermined 𝐾 value, there is no universally valid answer. K’s optimal value depends on the dataset and task.
There are numerous ways to find the optimal cluster number:
The Elbow Method
Choosing 𝐾 is commonly done using the Elbow Method. Apply the K-Means method with several values of 𝐾 and plot the sum of squared distances (inertia) within each cluster against the number of clusters. Inertia decreases with increasing 𝐾 , however the decline becomes less substantial at a certain degree. The ideal 𝐾 value is often the “elbow” of the plot, where the rate of decrease slows down.
Silhouette Score
Clustering quality is also assessed using the Silhouette Score. The data point’s similarity to its cluster compared to others is measured. Higher silhouette scores imply better-defined clusters, while lower scores indicate poorly separated clusters. Calculate the silhouette score for various 𝐾 values to determine the optimal value.
Gap Statistics
Gap Statistics evaluates K-Means clustering on real and random data. The optimal 𝐾 value optimizes the difference between real and synthetic data clustering results.
Advantages of K-Means
Numerous reasons make K-Means clustering popular:
- Simplicity: The algorithm is simple. Beginner machine learners can use it because it is one of the simplest clustering methods.
- Efficiency: K-Means is computationally efficient and scales well with huge datasets. For issues with many data points and features, it works well.
- Scalability: K-Means handles huge datasets well. Compared to other sophisticated clustering methods, it can cluster millions of data points quickly.
- Interpretability: K-Means results are straightforward. The data points are given to the nearest cluster centroid. This makes clusters easy to identify and visualize.
- Wide Applicability: K-Means can solve difficulties in customer segmentation, anomaly detection, image compression, and more.
Limitations of K-Means
The powerful algorithm K-Means has various drawbacks:
- Choosing K: A major problem with K-Means is selecting the number of clusters (𝐾) in advance. An erroneous choice of 𝐾 can lead to bad algorithm outcomes.
- Sensitivity to Initial Centroids: The algorithm is sensitive to initial centroids. Suboptimal clustering or convergence to a local minimum might result from weak initialization. Improved initialization methods like K-Means++ address this issue.
- Assumption of Spherical Clusters: In K-Means, spherical clusters are assumed to be about similar in size. Using K-Means with non-spherical or varying-sized or-density clusters may not work well.
- Handling Outliers: Outliers skew centroids and impact grouping in K-Means. Unrepresentative clusters may have outliers.
- Fixed Number of Clusters: To use the algorithm, specify the number of clusters (𝐾) before running it. When the appropriate cluster number is unknown or varies with dataset, this can be troublesome.
Applications of K-Means
K-Means clustering has a wide range of applications across various industries and domains:
- Customer segmentation: K-Means is used in marketing and business to segment customers by demographics, purchasing behavior, and other factors. This lets organizations personalize offers and marketing to different customer segments.
- Image Compression: K-Means clusters similar colors and replaces them with the cluster centroid. The compressed image retains most of its visual quality.
- Anomaly Detection: In K-Means, data points that do not fit into any cluster can be identified as anomalies or outliers. These data points may be rare.
- Document Clustering: K-Means is used in natural language processing (NLP) to cluster papers with similar subjects. It aids information retrieval, topic modeling, and recommendation systems.
- Geospatial Data Analysis: Urban planning and resource management benefit from K-Means’ ability to organize places by proximity or environmental characteristics.
Conclusion
Unsupervised learning and data analysis with K-Means clustering is effective. This clustering tool is popular due to its simplicity, scalability, and versatility. However, the approach is sensitive to initialization and outliers and requires pre-selecting the number of clusters. K-Means is a fundamental machine learning technique utilized in many applications despite these problems. Understanding K-Means’ benefits and drawbacks helps you apply it to real-world challenges and gain valuable data insights.
