A sophisticated kind of artificial neural network that belongs to the generative model family, Deep Boltzmann Machines (DBMs) are made to extract intricate patterns from massive datasets. Like an artist learns to produce new works of art based on a collection they have examined, their goal is to replicate the input data they are provided. DBMs are especially helpful for jobs that require comprehending complicated data, including text, music, or graphics.
What are Deep Boltzmann Machines (DBMs)?
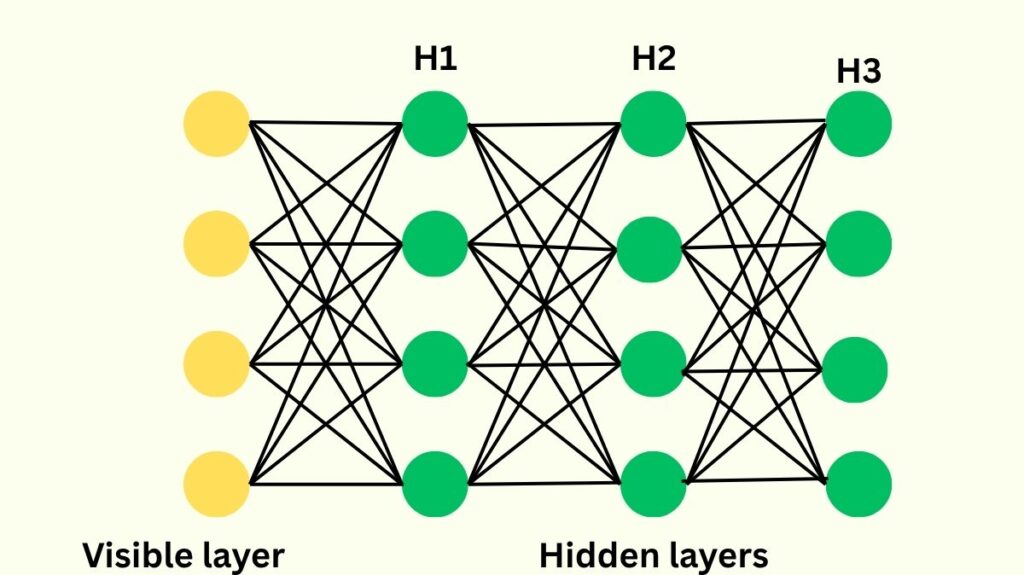
A computational model having several hidden layers with connections between nodes in all directions that is, undirected connections is called a Deep Boltzmann Machines (DBM). By using features taken from one layer as input to the next, this design enables DBMs to learn hierarchical features from raw data, creating representations that get more abstract over time. The word “deep” refers to these many levels, which allow for a thorough comprehension of the data. Each layer of a DBM functions as a building block for the extraction of latent characteristics, and they can be thought of as a stacked version of several RBMs.
Since DBMs give each potential network state a “energy” level, with lower energy states being more frequent, they are also referred to as energy-based models. Finding states that minimise this energy is a key component of the learning process. Their usage of stochastic neurones, which decide at random which neurones to activate depending on input and the condition of other network units, is one of their defining features.
Deep Boltzmann Machines (DBM) History
Boltzmann Machines (BMs) were first proposed by Hinton and Sejnowski in 1983. However, a number of computing limitations, including the lengthy learning process needed to estimate data-dependent and data-independent statistics using randomly initialised Markov chains, made the original BMs impossible to implement. This was made simpler by Smolensky’s (1986) Restricted Boltzmann Machine (RBM), which made inference simpler by prohibiting connections within the same layer.
Salakhutdinov et al. suggested Deep Boltzmann Machines, which built on RBMs. For generic Boltzmann machines, especially DBMs with numerous hidden layers, they created an effective learning process. Learning DBMs with millions of parameters is now feasible thanks to this innovative process. Originally, stacking RBMs gave rise to other deep architectures such as Deep Belief Networks (DBNs); however, DBNs have a hybrid architecture with directed connections in lower layers. DBMs set themselves apart by preserving undirected connections across their whole structure. The creation of DBMs sought to create generative and discriminative models that were faster and more stable while addressing issues with biassed gradient estimates.
Deep Boltzmann Machine (DBM) Architecture
A Deep Boltzmann Machine’s architecture is distinguished by:
- Several hidden layers: Deep Boltzmann Machines are made up of multiple hidden unit layers.
- Directionless connections: DBMs feature directionless connections between every node throughout every layer, in contrast to certain other neural networks or even Deep Belief Networks (DBNs).
- Stacked RBMs: In essence, the structure uses RBM connection to couple layers of random variables. With a visible layer and a hidden layer, but no connections within the same layer, an RBM is essentially a simpler Boltzmann machine.
- Layer arrangement: Inference has historically been unmanageable due to the fact that units are grouped in discrete layers and, in theory, units in odd-numbered levels are independent of units in even-numbered layers.
- Contrast with DBNs: One of the main architectural differences between DBNs and DBMs is that DBMs have undirected linkages all the way through, while DBNs only have undirected connections between their top two layers, with the lower layers constituting a directed generative model.
How Deep Boltzmann Machines Work?
Deep Boltzmann Machines go through several stages of learning:
Unsupervised Learning
DBMs mostly use unsupervised learning, which allows them to find patterns and structures in data without the need for direct labelling or direction. They essentially learn the probability distribution of the data by modifying the connections between units to resonate with its structure.
Pre-training at the layer level
- A greedy, layer-wise pre-training step usually precedes the training process. One layer at a time, a stack of Restricted Boltzmann Machines (RBMs) must be learnt.
- Because tiny random weights result in underconstrained hidden units and large random weights can impose substantial biases, it is important that the weights be initialized to sensible values during pre-training. Additionally, it aids in avoiding subpar local minima when learning.
- To address “double-counting” difficulties when top-down and bottom-up impacts are mixed, a modification is made during pre-training for the first and final RBMs in the stack. Bottom-up weights for the initial RBM must be twice as high as top-down weights. Top-down weights for the final RBM must be twice as large as bottom-up weights. When composing intermediate RBMs into the DBM, their weights are usually cut in half.
Approximate Inference
- To incorporate top-down feedback and speed up learning, DBMs employ an approximation inference process that involves an initial bottom-up pass. This first step effectively initialises the mean-field inference by using twice the weights to make up for the first run’s lack of top-down input.
- DBMs use a variational approximation, usually a fully factorized (naive mean-field) distribution, to estimate data-dependent statistics. This approach seeks to approximate the variational approximation and create a unimodal true posterior distribution over hidden variables.
- Persistent Markov chains are used by DBMs to estimate data-independent statistics. Because the learning process creates a dynamic change in the energy landscape, this approach enables the chains to explore the state space far more quickly than their mixing rates would have indicated.
- Repetitively modifying weights according to data-dependent and data-independent statistics is part of the learning process.
- Fine-Tuning: To better mimic the data, DBMs go through a fine-tuning phase after pre-training, during which all parameters are simultaneously changed. Using labelled data, such as backpropagation, this stage can be carried out discriminatively (under supervision).
- Data Generation: A DBM can produce fresh data after it has been trained. In order to update the pattern to match those discovered during training, it iteratively refines the initial random pattern.
Deep Boltzmann MachinesTraining Approaches and Solutions
DBMs are trainable despite their intractability. For effective learning with Deep Boltzmann Machines, for instance, a recognition model also known as an approximate inference model can be used. In essence, this method is comparable to stochastic backpropagation and Auto-Encoding Variational Bayes (AEVB).
Another online learning technique that works with continuous latent variable models is the “wake-sleep” algorithm, which uses a recognition model just like DBMs. Wake-sleep necessitates the simultaneous optimization of two objective functions that do not match the marginal likelihood, in contrast to the Variational Auto-Encoder (VAE) technique.
There are two stages in the general learning rule for Boltzmann Machines, which are the forerunner of DBMs:
Positive Phase: Hidden units are permitted to achieve thermal equilibrium while input units are clamped. Units’ co-occurrence statistics are quantified.
Negative Phase: Every unit functions independently without outside assistance. Co-occurrence statistics are measured once more.
The difference between the co-occurrence data from these two phases serves as the basis for the weight updates. A stochastic gradient ascent on the log-likelihood is what this technique essentially is.
Methods such as “simulated annealing,” in which the “temperature” parameter is gradually decreased, are employed to avoid local minima during training.
Advantages and disadvantages of DBMs
What are the advantages of DBMs?
DBMs provide a number of noteworthy advantages:
Hierarchical Feature Representation
Their proficiency in extracting hierarchical features from unprocessed data is important for comprehending intricate inputs.
Handling Ambiguity
By integrating top-down feedback into their approximation inference process, DBMs are better equipped to handle ambiguous inputs and resolve uncertainty around intermediate-level features.
Generative Power
DBMs are strong generative models that can pick up accurate data representations. For instance, they are able to produce 3D objects and lifelike handwritten numbers.
Classification and Retrieval Performance
They outperform models such as Support Vector Machines (SVMs), Latent Dirichlet Allocation (LDA), autoencoders, and in some cases, Deep Belief Networks (DBNs) in classification and information retrieval tasks.
Initialization for Feedforward Networks
When labelled training data is limited and unlabelled data is plentiful, learnt DBM weights can intelligently initialize deep feedforward neural networks, resulting in better discriminative performance.
Gain from Unlabelled Data
More unlabelled training data can be very helpful to them. This enhances generalisation by guaranteeing that the majority of the model’s information originates from modelling input data rather than merely a little amount of label information.
Image In-painting
DBMs show that they can infer occluded portions of images, even for objects that are not visible, in a cohesive manner.
What are the Disadvantages of DBMs?
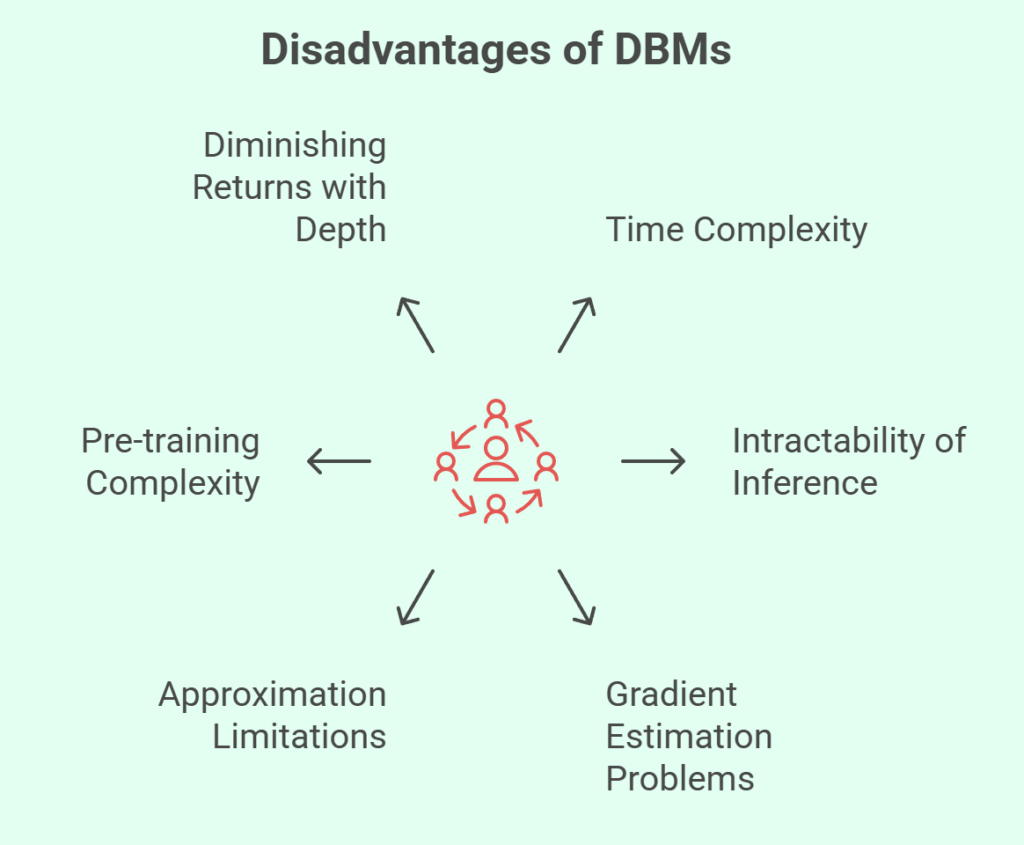
Notwithstanding their advantages, DBMs have certain disadvantages:
Time Complexity
Time complexity limitations may arise from choosing the best parameters for DBM training. Using sampling or variational methods can result in a delayed learning process overall.
Intractability of Inference
Exact inference is unachievable due to the undirected nature and relationships between odd and even layers. It is computationally impossible to determine the precise probability that a DBM gives to a visible vector without estimating the partition function.
Problems with Gradient Estimation
High variance in gradient estimates plagued the original Boltzmann machine learning, which would have driven parameters to unwanted areas. Although the learning process itself can still proceed, persistent Markov chains may have slow mixing rates.
Approximation Limitations
Because the gradient’s negative sign would lead the parameters to deviate from the approximation, variational approximations are not appropriate for estimating data-independent statistics.
Pre-training Complexity
Although useful, the pre-training approach necessitates unique adjustments for the initial and final RBM layers (doubling weights in a single direction). Furthermore, it has been observed that it is challenging to build a proof that ensures variational bound improvement for intermediate hidden layers.
Diminishing Returns with Depth
Because each additional layer in a DBM performs less “modelling work” than in a DBN, DBMs may see diminishing advances in the variational bound during the pre-training phase more quickly than DBNs.
Features of Deep Boltzmann Machines (DBMs)
- Generative Model: The main purpose of DBMs is to produce fresh data samples that closely resemble the training set.
- Probabilistic Representation: They capture feature interactions in a probabilistic manner by defining a probability density over the input space.
- Unsupervised Learning: Without clear labels, DBMs can identify patterns and structures in data.
- Hierarchical Feature Extraction: They extract features layer by layer, learning more abstract representations with each layer that comes after.
- Undirected Connectivity: All bidirectional (undirected) connections between layers enable rich feedback and interactions.
- Stacked RBMs: These machines are based on the basic Restricted Boltzmann Machine (RBM) architecture.
- Energy-Based Framework: They use an energy function to measure the “goodness” of a network state and learn to minimise it for likely states.
- Stochasticity: DBM neurones introduce randomness that can aid in data space exploration by making probabilistic decisions regarding activation.
- Complex, higher-order correlations between the activities of hidden features in successive layers can be learnt by DBMs through the use of higher-order correlation learning.
What are the different types of DBMs?
Although the sources mostly address the Deep Boltzmann Machine as a single model type, they emphasise differences in its setup or use rather than essentially distinct DBM types:
- Multi-layer Configurations: DBMs, such as two-layer or three-layer DBMs, are frequently described in terms of the quantity of concealed layers.
- Multimodal DBM (MM-DBM): This particular application uses DBMs to create a generative model of multimodal data, including text and images, which is helpful for information retrieval and categorisation across various data types.
- Binary versus Non-Binary Units: Although DBMs are mainly described in relation to binary units, the learning techniques may be applied to DBMs constructed using RBM modules that carry tabular, count, or real-valued data as long as the distributions are members of the exponential family. For example, greyscale images can be modelled using Gaussian-Bernoulli RBMs.
DBMs vs DBNs
In contrast to DBNs vs DBNs:
- Deep learning algorithms constructed from stacked RBMs are known as DBMs and DBNs.
- Their connectivity is the main architectural difference: DBMs have undirected connections across their whole structure, while DBNs have a hybrid structure with directed top-down connections in lower layers and undirected connections only between their top two layers.
- DBM pre-training, with its modified RBM stacking, replaces only half of the prior during pre-training, whereas DBNs replace the complete prior over the previous top layer. This suggests that the lower layers in DBMs may be subjected to greater modelling effort.
- In contrast to DBNs, DBMs’ approximation inference process can include top-down feedback following an initial bottom-up pass, which increases their resilience to ambiguous inputs.
Also Read About An Introduction To Restricted Boltzmann Machines Explained
Important Ideas in DBM Operation
- Energy Function: The “energy” of a joint configuration of visible and concealed nodes is measured by this mathematical function. Finding weights that minimise this energy and increase the likelihood of the observed data is the aim of learning.
- Partition Function: A Boltzmann distribution normalization constant that guarantees all probabilities add up to one. In DBMs, its precise computation is frequently unfeasible, necessitating the use of approximation techniques such as Annealed Importance Sampling (AIS).
- Contrastive Divergence (CD): A greedy layer-wise pre-training technique for DBMs that is also used to efficiently train RBMs. Faster learning is made possible by its biassed yet low-variance gradient estimates.
- Gibbs Sampling and Markov Chain Monte Carlo (MCMC): These sampling methods are essential to DBMs. By iteratively sampling unit activations, they are utilized to explore the state space of the network and derive data-independent statistics.
- Variational Inference: This method uses a more straightforward, tractable distribution (similar to a mean-field approximation) to approximate the genuine posterior distribution over latent variables. By reducing the difference between the real and approximate posteriors, it helps to regularize learning and is employed for estimating data-dependent statistics.
Applications of DBMs
- Informatics in Health
- Applications for Cybersecurity
- Visual Knowledge
- Denoising of images
- The use of hierarchical feature representation in the early diagnosis of mild cognitive impairment (MCI) and Alzheimer’s disease (AD).
- Object and Speech Recognition
- Wearable and mobile sensor networks for human activity recognition.
- Topic modelling, which surpasses LDA.
- Multimodal learning, which includes both text and visuals.
- The detection of spoken queries.
- The most advanced 3D model recognition technology.
- Modelling faces.
Promising outcomes have been demonstrated by Deep Boltzmann Machines; for instance, they achieved an error rate of 0.95% on the MNIST test set (permutation-invariant version), which was the best published result at the time of the publication. DBMs obtained a misclassification error rate of 10.8% on the NORB dataset, a more challenging job containing 3D toy items; this percentage was further decreased to 7.2% with enriched unlabelled training data. They can also successfully restore portions of images that are obscured.
Also Read About Gaussian Restricted Boltzmann Machine And Binary RBM
