Here, we’ll talk about what backpropagation is and how it operates. This section covers the following topics: backpropagation’s history, neural network architecture, key concepts and features, types of backpropagation, advantages, disadvantages, and applications.
An essential machine learning method for training artificial neural networks is backpropagation. It is mostly a gradient computing technique for figuring out how to update a neural network’s parameters as it is being trained.
What is backpropagation and how does it work?
What is backpropagation in neural network?
Backpropagation, which stands for “backward propagation of error,” is an artificial neural network optimization technique. By modifying the weights and biases inside the network, its primary objective is to lessen the discrepancy between the output that the model predicts and the output that is actually obtained. The chain rule from calculus is effectively applied to neural networks, enabling it to efficiently travel intricate layers in order to minimize the cost function. The phrase is sometimes used broadly to refer to the complete learning method, including the phase of altering model parameters, even though it really only relates to the algorithm for effectively computing the gradient.
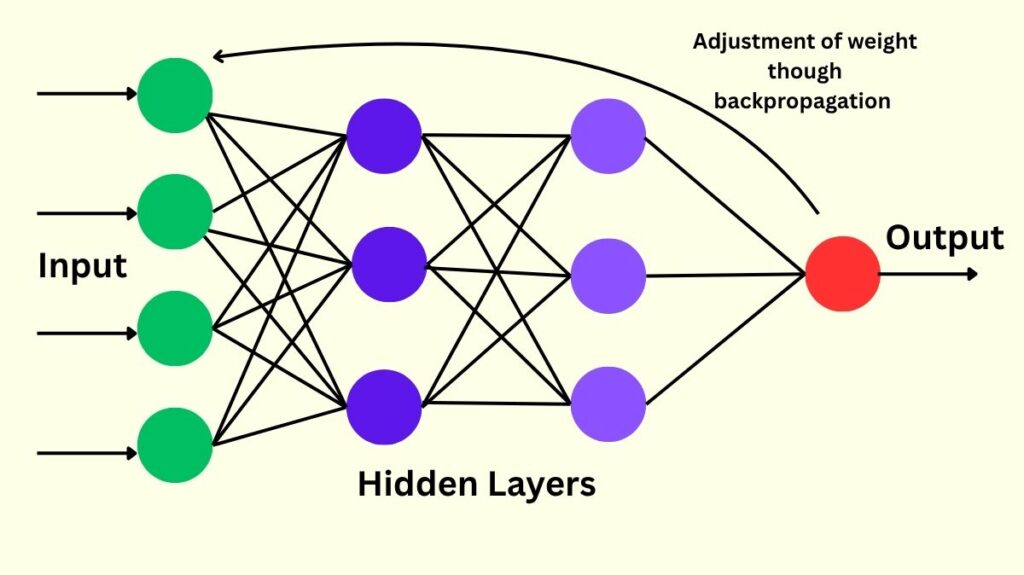
How does backpropagation work
The Forward Pass and the Backward Pass are the two primary steps of the backpropagation algorithm.
Forward Propagation, or Forward Pass
- The input layer receives input data, which is then mixed with the appropriate weights and sent layer by layer through the network.
- An activation function is used to each neuron to provide an output after the weighted sum of inputs has been determined.
- The subsequent layer uses the output of the previous layer as its input. Until the output layer generates a final forecast, this process keeps on.
- For usage in the backward pass, intermediate values such as the weighted inputs and activations are cached during this phase.
Loss Function Calculation
- Following the forward pass, a loss function (also known as a cost function or error function) calculates the difference between the target output for a particular training example and the network’s projected output.
- Inaccuracy is quantified by the loss function, and different formulas are appropriate for different tasks (e.g., cross-entropy for classification, squared error for regression).
- Finding the function (i.e., the collection of weights and biases) that minimizes this mistake reduces the network training problem to an optimization problem.
Also Read About What are the Radial Basis Function Networks?
Error backpropagation, or backward pass
- The phrase “backpropagation” is strictly applicable in this situation. Beginning at the output layer, the error determined by the loss function is spread backward across the network.
- The gradient of the loss function with respect to each weight and bias in the network is efficiently computed using the chain rule of calculus. This indicates the relative contribution of each parameter to the total error.
- By iterating backward, layer by layer, the computer essentially computes the gradient for each layer from back to front, avoiding superfluous calculations. Compared to calculating each derivative separately, this is far more efficient.
Updated Parameters for Gradient Descent
- After the gradients are calculated in the backward pass, the network’s weights and biases are adjusted using an optimization approach such as gradient descent (or stochastic gradient descent).
- To reduce the error, the objective is to descent (move down) the gradient of the loss function. The gradient shows which way to change the settings in order to minimize loss.
- Learning Rate: The learning rate is a hyperparameter that regulates the magnitude of each adjustment step. For successful and efficient training, a well-chosen learning rate that strikes a balance between speed and the possibility of exceeding the minimum is essential.
- Batch Size: There are various methods for updating weights: Batch gradient descent: Before changing parameters, gradients are calculated for every training example. One training example is used for every update in stochastic gradient descent (SGD), which produces faster but possibly more erratic convergence.
- Mini-batch gradient descent: Provides a compromise between the other two methods by updating weights using a small batch of training instances.
- This iterative process of forward pass, backward pass, error calculation, and parameter updating keeps going until the error converges to a minimum or the desired result is obtained.
History of Backpropagation
The history of backpropagation is complex and full of both incomplete and many discoveries.
Forerunners
Gottfried Wilhelm Leibniz first proposed the fundamental idea, which is an effective use of the chain rule, in 1676. Frank Rosenblatt coined the concept “back-propagating error correction” in 1962, but he was unsure of how to apply it Additionally, beginning in the 1950s, precursors to optimal control theory were identified by individuals such as Pontryagin, Henry J. Kelley (1960), and Arthur E. Bryson (1961). In 1962, Stuart Dreyfus offered a more straightforward derivation based on the chain rule. The first multilayer perceptron trained using stochastic gradient descent was presented by Shun’ichi Amari in 1967. The ADALINE algorithm (1960) employed gradient descent for a single layer.
Modern Backpropagation
Described as the “reverse mode of automatic differentiation” for discrete connected networks of nested differentiable functions, modern backpropagation was initially reported by Seppo Linnainmaa in 1970. After developing backpropagation for his doctoral thesis in 1971, Paul Werbos extended it to Multilayer Perceptron(MLPs) in the conventional manner in 1982. Backpropagation was independently invented around 1982 by David E. Rumelhart, Geoffrey Hinton, and Ronald J. Williams. They published their extremely influential publications in 1985 and a 1986 Nature paper that greatly aided in the popularization of the technique. The technique was also explained by David Parker in 1985.
Obstacles to Acceptance
The widely held notion at the time that neurons produced discrete, not continuous, signals that would make gradient computation impossible, as well as the lack of assurances to establish a global minimum (only a local minimum), were among the first criticisms.
Resurgence
Backpropagation gained popularity again in the 2010s after losing ground in the 2000s, due to the development of affordable, potent GPU-based computer systems.
Neural Network Architecture in Backpropagation
Artificial neural networks, which closely resemble the structure of the human brain, are the basis for backpropagation.
Nodes (Neurons)
Layers of interconnected computational units are called nodes, or neurones. An activation function is a mathematical operation that each neurone applies to the total of its weighted inputs.
Layers
- Input Layer: Acquires the initial data, usually in the form of a vector, with each input neuron representing an input feature.
- Hidden Layers: The majority of “learning” takes place in these layers, which are in between the input and output layers. Neurons’ in one layer of a typical feedforward network are connected to every other neuron in the layer directly below.
- Output Layer: This is where the network makes its final predictions.
- Weights: The significance of a neuron’s contribution to a neuron in the following layer is determined by the weight, which is a unique multiplier assigned to each connection between two neurons. Backpropagation is used to optimize these movable parameters.
- Biases: The sum of the weighted inputs that a neuron receives may additionally contain a bias, which is a constant number. Backpropagation also optimizes adjustable parameters called biases.
- Activation Functions: The weighted sum of inputs at each neuron is subjected to non-linear and differentiable mathematical functions known as activation functions. They add non-linearity, which allows the model to generate gradients that can be optimized and capture intricate patterns. Sigmoid, tanh, and ReLU (Rectified Linear Unit) are typical examples, as is softmax for classification in the final layer.
Also Read About What Is Single Layer Perceptron Neural network Architecture
Features and Key Concepts of Backpropagation
Several fundamental characteristics define backpropagation:
- Gradient Computation: Its main purpose is to calculate a loss function’s gradient in relation to the weights of the network.
- Chain Rule Application: This is a productive use of the calculus chain rule.
- Iterative Process: In order to minimize the cost function, iteratively adjusts weights and biases across a large number of training samples (epochs).
- Dynamic Programming: Dynamic programming can be used to calculate gradients efficiently by avoiding unnecessary computations using backward iteration.
- Reverse Mode of Automatic Differentiation: One subset of this larger family of methods is backpropagation.
- Optimization Algorithm: It is the foundation of optimization algorithms used to train neural networks, such as gradient descent.
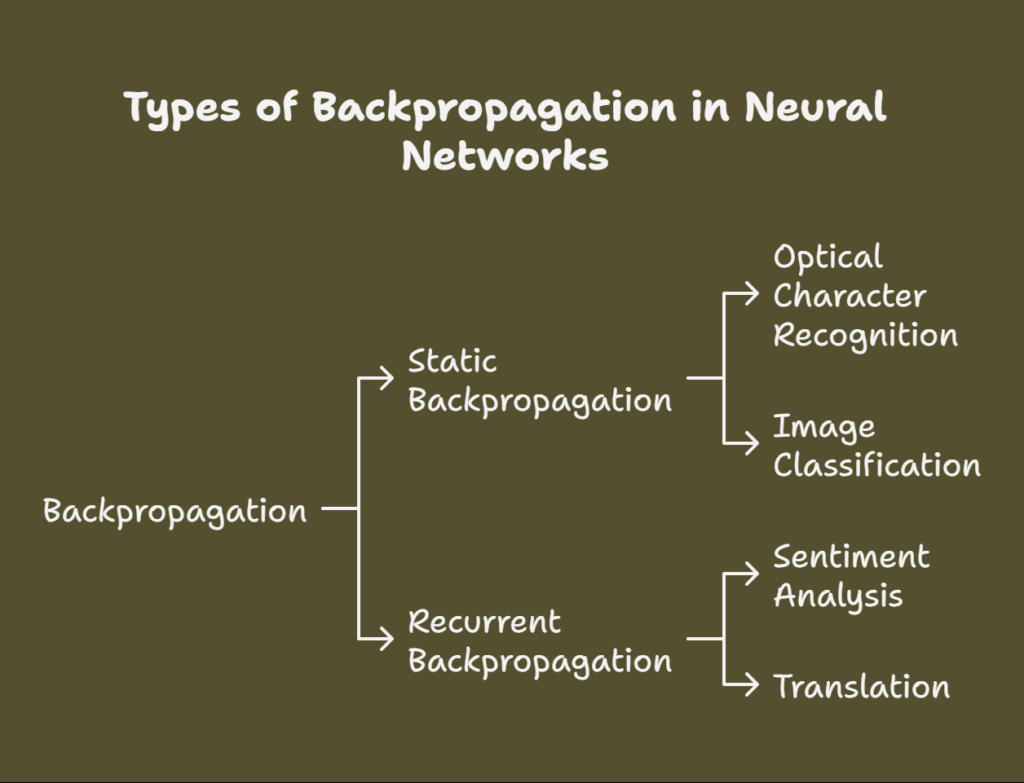
Types of backpropagation
Although backpropagation is a gradient computing process in and of itself, it is utilized in a variety of neural network designs and in combination with other optimization algorithms.
In neural networks, backpropagation comes in two main forms:
Static Backpropagation
This kind is employed in feedforward neural networks, in which data moves from input to output in a single direction. It is used to solve issues with fixed inputs and outputs, such optical character recognition (OCR) and picture classification, where the output is generated instantly upon input.
Recurrent Backpropagation
For fixed-point learning, this kind is used in recurrent neural networks (RNNs), frequently in time-series models. Activations are fed forward in recurrent backpropagation until a fixed, stable value is reached. To correct for weights and biases, the error is then computed and propagated backward. This kind of problem is employed in natural language processing tasks like sentiment analysis and translation, where the input and output may alter over time.
The main distinction between the two is essentially in how they are used: recurrent backpropagation deals with issues involving sequential data and time-dependent relationships, whereas static backpropagation tackles static input-output mappings.
Network Architectures
- Training different kinds of neural networks requires backpropagation.
- The fundamental scenario in which information goes in a single direction is feedforward neural networks.
- Recurrent neural networks (RNNs): Specific variants such as “Backpropagation Through Time” are utilized for sequential data.
- A common tool for image processing is the Convolutional Neural Network (CNN).
- Networks with several hidden layers that mostly rely on backpropagation for training are known as deep neural networks.
Advantages of backpropagation
Backpropagation provides a number of significant advantages for neural network training:
- Efficiency: By immediately updating weights depending on error, it calculates the gradient of the loss function rapidly, speeding up learning, particularly in deep networks.
- Scalability: Deep learning is made possible and perfect for large-scale jobs by the algorithm’s strong scalability to networks with numerous layers and intricate designs.
- Automated Learning: Without human involvement, the model may adapt to maximise performance by automating the learning process.
- Generalisation: It increases prediction accuracy by assisting models in making good generalizations to new, unknown data.
- Implementation Ease: By modifying weights using error derivatives, it makes programming simpler and is regarded as beginner-friendly.
- Flexibility and Simplicity: Due to its uncomplicated design, it can be applied to a variety of tasks, ranging from simple feedforward networks to more intricate convolutional or recurrent networks.
Disadvantages of backpropagation
Backpropagation has various disadvantages despite its advantages:
- Local Minima: Gradient descent with backpropagation may converge to a local minimum rather than the error function’s global minimum. Additionally, it has trouble handling plateaus in the landscape of the error function.
- Derivative Requirement: In order to use backpropagation, the network’s activation functions must be differentiable.
- Vanishing Gradient Problem: As gradients propagate backward in very deep networks, they can get quite tiny, which hinders the ability of earlier layers to learn efficiently. This is typical of activation functions such as tanh or sigmoid.
- Exploding Gradients: On the other hand, if gradients get too big, the network’s training will diverge.
- Overfitting: A neural network may perform poorly on fresh data if it is overly complex for the available data, memorizing the training set rather than identifying patterns that can be applied to other data.
- Input Normalization: Normalizing input vectors might enhance performance, however it is not necessarily necessary.
Applications of backpropagation neural network
- Self-supervised, semi-supervised, and supervised learning.
- Early achievements such as ALVINN for autonomous driving and NETtalk for text-to-pronunciation.
- Various jobs in chemical research and development, include reading infrared spectra and predicting protein secondary structures.
- Current applications in speech recognition, machine vision, and natural language processing.
- Addressing issues such as the XOR function.
