What is a Markov Chains?
Systems that change between several states, according to probabilistic criteria are described by Markov chains, a potent mathematical framework. Markov chains model systems that change condition in phases. Probabilities can define these systems’ overall behavior, but their details are unpredictable.
Imagine playing a board game where die rolls determine moves. Your chances of advancing forward, backward, or keeping still depend on where you are on the board. Importantly, your future move depends only on where you are now, not on your previous moves. Markov chains work this way.
System “state” is its present state. The “transition” is between states. The “chain” stems from these transitions happening sequentially like links.
Understanding the Markov Property
A important principle of Markov chains is the “Markov property.” This means that the next step in a process depends on the current state, not how you got there.
Imagine trying to forecast tomorrow’s weather. Applying the Markov property means that tomorrow’s weather depends only on today’s weather, not on prior days’ weather. If today is sunny, tomorrow may be sunny, cloudy, or rainy. Markov chains simplify complex processes and make helpful predictions by focusing on the current state.
Period of a markov chain
The Russian mathematician Andrey Markov discovered the basic ideas of Markov chains in the early 1900s; his first work on the subject was published in 1906.
In order to create a weak law of large numbers without the independence assumption, Markov, who was interested in extending independent random sequences, demonstrated that, in specific circumstances, the average outcomes of a Markov chain would converge to a fixed vector of values. Later, he used Markov chains to examine how vowels and consonants are distributed in literary works like “Eugene Onegin” by Alexander Pushkin.
Also Read About What is sparse decomposition? and its Fundamental Goals
Additional early innovations and uses consist of:
- Prior to Markov’s work, Poisson processes continuous-time Markov processes were identified.
- In 1907, Paul and Tatyana Ehrenfest presented a diffusion model.
- A branching process that predates Markov’s work was examined by Francis Galton and Henry William Watson in 1873. Decades ago, Irénée-Jules Bienaymé had independently discovered this branching mechanism.
- In 1912, Henri Poincaré examined card shuffling by studying Markov chains on finite groups.
- In 1938, Maurice Fréchet published his thorough research on Markov chains.
Core Concepts and How it Works
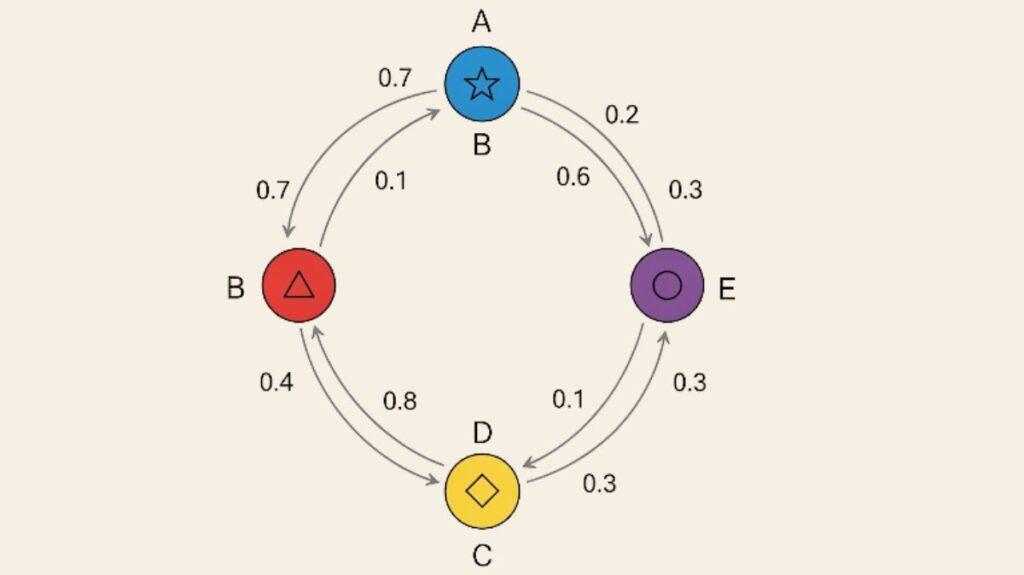
A Markov chain is a model for a system that alternates between various “states” or circumstances. The state space is the collection of all conceivable states.
Transitions and Transition Probabilities
There are particular probabilities associated with the system changing states or even remaining in the same state. State transition probabilities are what these are known as. For instance, if a system has two states (A and E), it may remain in state A with a probability of 0.6 or transition to state E with a probability of 0.4.
Transition Matrix
- A transition matrix is a useful tool for representing a Markov chain.
- This is a square matrix, with each column representing the future state and each row representing the current state.
- The likelihood of changing from the state of the row to the state of the column is represented by the value in each cell.
- Since the transition matrix shows the entire probability distribution from a state, each row adds up to 1.
- The transition matrix for a system with N states is always N x N.
Initial State Vector
The initial probabilities for each state are specified by a N x 1 initial state vector.
N-Step Transition probability
The transition matrix is raised to the power of N (for N steps) in order to determine the probability of transitions over a number of steps. The likelihood of switching between states in that many steps is then displayed by the entries in the resulting matrix.
Time-Homogeneous
Markov chains can be used to simulate a random walk, in which the transition probabilities of the current state are used to randomly select the next state. This is a good example of the memoryless property.
Stationary Distribution
This shows the likelihood of staying in each state over the long term, regardless of where you start. It is equivalent to the transition matrix’s eigenvector linked to eigenvalue 1. This distribution provides the percentage of time the Markov chain spends in different states over time.
Also Read About Stochastic Gradient Variational Bayes and its Advantages
Fundamental Properties and Features
A Markov chain’s behaviour is described by a number of properties:
Irreducibility
Markov chains are irreducible if any state can be reached from any other, possibly over several steps. This indicates that every state i in its state transition diagram has a path to every other state j. A finite Markov chain has a unique stationary distribution and all of its states are positive recurrent if it is irreducible.
Periodicity
If a state may only be returned at multiples of a step larger than 1, it is said to be periodic. The state is aperiodic if this step is 1. An irreducible Markov chain is aperiodic if it contains a single aperiodic state.
Recurrence and Transience
- Transient States: This state may never be reached again by the system.
- Recurrent States: At some point, the system will undoubtedly return to this condition. If a finite chain is irreducible, then every state is recurrent.
- Positive Recurrent: If a recurrent state is anticipated to return in a finite number of steps, it is said to be positive recurrent. Positive recurrence is the same as the presence of a stationary distribution for irreducible chains.
- Null Recurrent: If the mean return time of a recurrent state is unlimited, it is null recurrent. In this instance, the long-term chance of discovering the chain at any given state is zero.
Absorbing States
There are no outgoing transitions from an absorbing state once the process has entered one.
Ergodicity
A state is ergodic if it is positive repeating and aperiodic. A Markov chain is ergodic if every state is. Reducible, aperiodic ergodic Markov chains converge to stationary distributions.
Time-Homogeneous
Time-homogeneous Markov chains have the same probability for state changes regardless of time. The transition matrix remains constant after each step.
Time Reversal
When time is run backwards for a Markov chain in equilibrium (i.e., begun from its stationary distribution), a new Markov chain is produced, however its transition matrix may differ. This idea is connected to intricate balance formulas. A chain is said to be reversible if it meets rigorous balance requirements.
Also Read About Types Of Backpropagation & Disadvantages Of Backpropagation
Types of Markov Chains
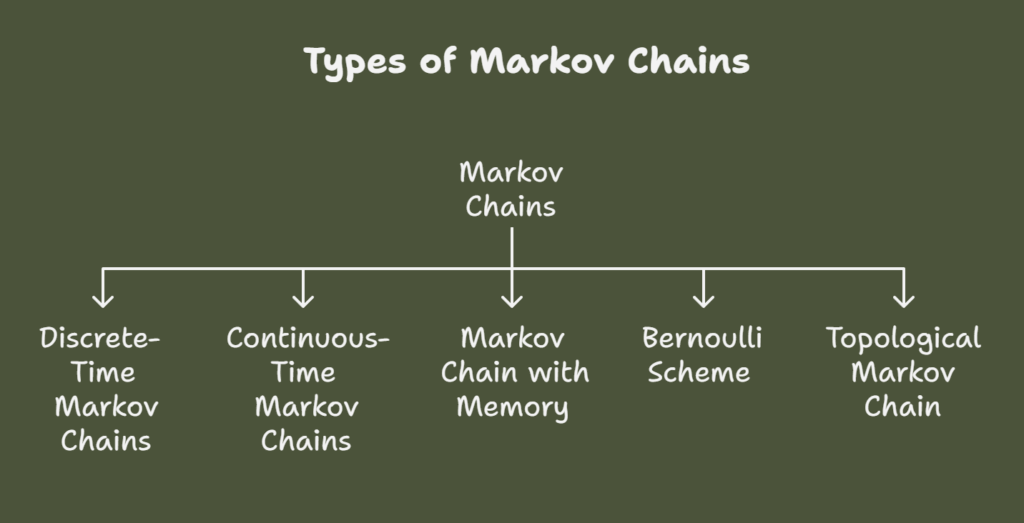
Markov chains can be divided into the following categories:
Discrete-Time Markov Chains (DTMC)
Discrete-Time Markov Chains (DTMC) are the most common type of Markov chains, where state transitions occur at predefined, countable time intervals. Most references to the “Markov chain” presume discrete time by default.
Continuous-Time Markov Chains (CTMC)
These chains allow for state changes to occur at any time because time is treated as continuous. They are often defined using an initial probability distribution and a transition rate matrix. The time between transitions for these processes is a random variable with the same distribution that is independent and exponential.
Markov Chain with Memory (Higher-Order Chains)
Higher-order chains, or Markov chains with memory, depend on the past m states to determine the future state when m is finite. This can be reformulated as a “classical” Markov chain by introducing ordered m-tuples of prior values into the state space. For instance, a second-order chain may consider both the current and previous states.
Bernoulli Scheme
A special case where the next state is completely independent of the current state and the transition probability matrix contains identical rows.
Topological Markov Chain (Subshift of Finite Type)
One type of shift that occurs when the adjacency matrix of a finite graph is substituted for the Markov matrix is the Topological Markov Chain (Subshift of Finite sort).
Advantages and disadvantages of markov chain
Advantages of markov chain
Modelling dynamic systems with Markov chains has several advantages.
- Simplicity: Because transition probabilities have straightforward mathematical formulas, they are easy to model and explain once they are established.
- Memorylessness: The Markov characteristic often works well with real-world systems where the current state alone determines the future. This important feature facilitates analysis.
- Computational Efficiency: Multi-step transitions, stationary distributions, and future probabilities may all be calculated efficiently thanks to matrix algebra.
- They serve as the foundation for more intricate frameworks like Hidden Markov Models (HMMs) and Markov Decision Processes (MDPs), which are essential in robotics, AI, and speech recognition.
- Any number of states and transition matrices can be used to model a wide range of systems.
Also Read About A Practical Guide To Training Restricted Boltzmann Machines
Disadvantages of markov chain
Markov chains have advantages but disadvantages.
- The constant transition probabilities implied by traditional Markov chains might not accurately represent reality.
- Discrete States: Classical Markov chains cannot be applied to continuous variable systems that have countable or finite states.
- Without higher-order chains, they are unable to replicate long-term dependencies or delayed effects.
- State Space Explosion: It might be difficult to interpret and compute when a system with a lot of features or states rapidly has a lot of possible states.
- Uncommon changes: It could be challenging to determine the likelihood of uncommon state transitions when there are more states.
- Subjectivity of Time Steps: Time steps in current models are frequently preset and can be selected at random. A coarse interval might miss significant variations.
- “Wait” Time Distribution: Because the fundamental model assumes that “wait” times (consecutive self-transitions) have a geometric distribution, it might not be suitable for all situations. Alternatively, embedded Markov chains are offered, which control “wait” times in a user-specified way.
Applications of markov chains
Markov chains are widely used in a variety of domains due to their ability to accurately replicate dynamic systems and sequential data.
Web Search (PageRank Algorithm)
Random page surfing and Markov chains are used in Google’s PageRank algorithm.
Natural Language Processing & Speech Recognition
HMMs are used in speech recognition, voice assistants, text modelling, and predictive typing.
Finance and Economics
Economics and finance model risk, credit ratings, company cycles, and stock prices.
Biology and Genetics
Phylogenetics, neurobiology, population dynamics, protein structures, genetic sequence modelling, and disease transmission are among the fields with applications.
Markov Chain Monte Carlo (MCMC) Methods in Statistics and Simulation
MCMC is a key element of modern statistical methods, using Markov processes to sample complex probability distributions for Bayesian inference, machine learning, and physics.
Physics
In statistical mechanics (Ising model), thermodynamics, and lattice QCD simulations, Markovian systems characterise uncertain system features.
Chemistry
In silico models of reaction networks, fragment-based chemical production, and enzyme activity (e.g., Michaelis-Menten kinetics).
Queueing Theory
Markov chains offer the theoretical underpinnings for understanding queues, which is crucial for optimizing telecommunications networks where messages compete for limited resources.
Software engineering and testing
By simulating system behaviour and usage profiles, they can develop test cases and assess system reliability.
Social Sciences
Used to explain path-dependent arguments, such as how democratic regimes replace autocratic ones as economies grow.
Music
Markov chains can be used to create music where the next note or phrase depends probabilistically on the one before it. Higher-order chain results can be more structured.
Sports and Games
Many games of chance, including Snakes and Ladders, can be accurately represented by Markov chains. They are also used to evaluate runs scored and analyse game conditions in advanced baseball analysis.
Markov Text Generators
Based on a sample document, these provide the basis for parody-generating software by employing Markov processes to generate text that is ostensibly legitimate.
Forecasting
Markov chains are used in a number of forecasting models, including those for price trends, wind power, terrorism risk, and sun irradiance.
Occupant Behaviour Models
By predicting patterns of behavioural states in buildings, these models offer precise representation and long-term predictions.
Anomaly Detection
They can be used to predict anomalies in places with high concentrations of people.
Also Read About What is Deep Generative Models? and its types
