What is an Echo State Networks? and Advantages of ESNs

Echo State Network Tutorail

Processing sequential and time-dependent data is a significant difficulty in the fields of machine learning and artificial intelligence. Problems with traditional recurrent neural networks (RNNs) include high computing costs and disappearing gradients. One reservoir computing model that provides a sophisticated solution to these issues is Echo State Networks (ESNs). Echo State Networks require little training effort and interpret temporal data quickly by utilizing a fixed, randomly linked “reservoir” of neurons.

What is Echo State Network?

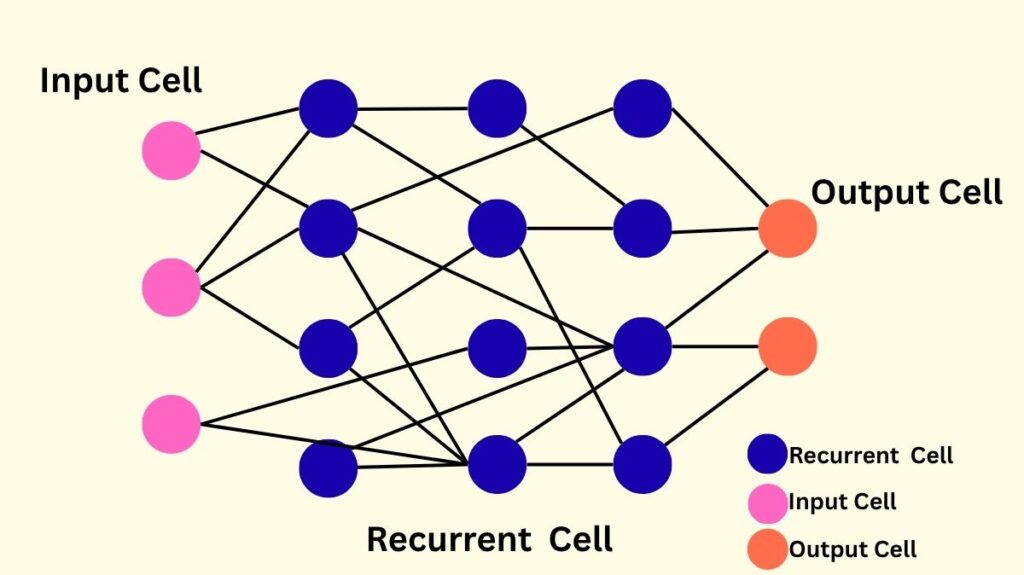
One kind of recurrent neural network (RNN) intended for processing sequential input is called an Echo State Networks (ESN). ESNs employ a fixed, randomly initialized reservoir of neurons that nonlinearly alters input signals, in contrast to conventional RNNs, which necessitate intensive training of every link. ESNs are significantly faster and simpler to utilize because only the output layer is trained.

History and Background

In the past ten years, reservoir computing which includes Echo State Networks has become a viable substitute for gradient descent techniques in recurrent neural network training. In 2002, the Echo State Network was initially proposed. Liquid State Machines (LSMs), which Wolfgang Maass developed independently and concurrently, are closely related to the fundamental idea underpinning ESNs. In general, reservoir computing encompasses ESNs, LSMs, and the backpropagation decorrelation learning rule for RNNs.

Due to problems like lack of auto differentiation, vulnerability to vanishing/exploding gradients, and the difficulty of modifying their connections, recurrent neural networks were rarely used in practice prior to the advent of Echo State Networks. Convergence was not assured by the slowness and susceptibility of traditional RNN algorithms to issues like branching faults. These problems were resolved by ESNs, which early on showed strong performance on time series prediction tasks from synthetic datasets.

Echo State Networks Architecture

Typically, an ESN has three primary layers:

Input layer: The sequential input data is received by the input layer, where each input represents a time step in the series.

Hidden Layer: Comparable to a “pool” of interconnected neurons, the Hidden Layer (Reservoir) is a unique component of the ESN. These hidden neurons have fixed and randomly assigned weights and connections. Internal neurons may not be completely connected since the reservoir is frequently sparsely connected. This layer is in charge of producing a nonlinear embedding of the input and projecting the data into a higher-dimensional space. The hyperbolic tangent (tanh) is one of these neurones’ common activation functions.

Output Layer: This layer produces the ultimate output for the network. ESNs are unique in that they solely train the output layer’s weights. Usually, a linear combination of the reservoir states is the output.

Also Read About What is BackPropagation Through Time, And BPTT Mechanism

How Echo State Networks Work

An ESN’s “reservoir” is a fixed, randomly initialized recurrent layer that is crucial to its operation. This reservoir efficiently collects and reproduces temporal patterns in sequential input to its echo-like dynamics.

Reservoir as Dynamic Memory

The network’s current state is determined by its recent input history, which is known as the echo state attribute.
Neurones with random weights and sparse connections make up the reservoir.
The reservoir encodes previous inputs by producing a rich, time-varying response when an input sequence is fed in.

Training

ESNs have a particularly straightforward training procedure. ESNs only change the weights of the output layer, as opposed to standard RNNs, which change all of the weights. This is as a result of the reservoir weights staying constant. Mapping the reservoir states to the intended output is part of the training process. Since this optimization’s error function is quadratic, it can be easily differentiated and solved as a linear system. To compute the output matrix, techniques like Ridge regression and linear regression are frequently employed.

Prediction

After training, the ESN makes predictions based on the patterns it has learnt. If the ESN is trained with a backshifted version of the output, it can function independently for signal production or prediction by using its prior output as input.

The reservoir’s memory capacity determines the required length of the initial “washout” phase, which is frequently used to adjust the reservoir’s starting values to the provided dataset using initialization data.

Also Read About The Power of Artificial Neural Networks in Data Science

Echo State Network Benefits

ESNs are appealing for a range of applications due to their numerous advantages:

Easy and Effective Training: Since the reservoir weights are fixed and only the output weights need to be trained, the ESN training process is very effective. They are therefore computationally efficient, particularly for jobs involving time-series prediction.
Memory Capacity: Because ESNs have built-in memory, they can recognize and retain temporal connections in sequential data.
Nonlinearity: By introducing nonlinearity through activation functions (such as tanh), the reservoir allows the network to model intricate correlations in data that may be difficult for linear models to capture.
Robustness to Noise: Because the dynamics of the reservoir can weed out irrelevant information, ESNs are renowned for their resilience to noise in input data.
Universal Approximator: ESNs can theoretically approximate any dynamical system, which makes them adaptable for a variety of uses.
Simplicity of Implementation: With the help of machine learning frameworks and libraries like NumPy, implementing ESNs is very simple.
Prevents Gradient Issues: The vanishing/exploding gradient issue, which afflicted conventional RNNs by resulting in either little parameter change or numerical instability and unpredictable behavior, does not affect ESNs.
Effective with Chaotic Time Series: Unlike standard neural networks, ESNs are not affected by bifurcations and are capable of managing chaotic time series.

Echo State Networks’ drawbacks

ESNs have several disadvantages despite their benefits:

Limited Control Over Reservoir Dynamics: Because the reservoir weights are fixed and initialized randomly, there is little direct control over its dynamics, which might make it difficult to customize the network for certain tasks.
Hyperparameter Sensitivity: ESNs depend on adjusting hyperparameters such the activation function selection, input scaling, spectral radius, and reservoir size. It frequently takes trial and error to find the ideal set of hyperparameters, which can be time-consuming.
Lack of Theoretical Understanding: ESNs’ theoretical understanding is less developed than that of some other neural network architectures, which makes it more difficult to forecast how they will behave in particular scenarios.
Limited Expressiveness: In certain situations, ESNs may struggle with jobs requiring extremely complex patterns and may not be as expressive as more sophisticated recurrent neural network architectures (such as LSTMs or GRUs).
Overfitting Potential: ESNs are susceptible to overfitting, particularly when training with sparse data, depending on task complexity and reservoir size.
Memory for complicated jobs: Reservoir computing techniques occasionally need an excessive amount of memory in order to do jobs that are as complicated as those handled by contemporary deep learning RNNs.

Variants of Echo State Networks

ESNs can be constructed in a number of ways, resulting in multiple variations:

Input-to-Output links: Directly trainable links between the input and output layers can be incorporated into the architecture of ESNs.
Feedback from the output back into the reservoir can be included or excluded.
Neurotypes and connection: The reservoir may contain a variety of neuron types and internal connection patterns.
Output Weight Calculation: A variety of offline and online techniques, such as support vector machines, margin maximization criteria, and linear regression, can be used to determine the output weights.
Hybrid and Continuous-Time ESNs: Some variations, such as those that partially integrate physical models, hybrid ESNs, and continuous-time ESNs, modify the formulation to better fit physical systems.
Deep ESNs: The Deep ESN model is a more recent invention that attempts to integrate the advantages of ESNs and deep learning.
Other specialised variants include Time Warping Invariant ESNs, ESNs with Trained Feedbacks, Long Short-Term ESNs, Auto reservoirs, Echo State Gaussian Processes, and Echo State Networks with Filter Neurons and a Delay and Sum Readout.
Quantum Echo State Networks: These are thought to be ubiquitous and are defined over nodes using qubit registers. Fascinatingly, the echo state property and fading memory in these networks can be advantageously induced by intrinsic noise in quantum computers.

Echo State Network Applications

ESNs are useful in many applications, especially those that include complex temporal relationships:

Time Series Prediction: This is the main area in which ESNs are particularly effective. It includes forecasting future values in chaotic time series and sequences with intricate patterns, such stock prices or weather patterns.
Signal Processing: ESNs are employed in telecommunications and engineering for signal treatment.
Control systems are used for a variety of control functions.
Speech Recognition: ESNs have been modified to recognize speech.
Predicting User Mobility and Content Popularity: Next-generation edge networks use them to forecast user mobility and content popularity, which aids in D2D (Device-to-Device) network cache placement optimization.
Industrial and Medical Applications: In a variety of industrial, medical, economic, and linguistic domains, ESNs have proven to be exceptionally proficient in sequence tasks.
Biological System Modelling: This covers memory modelling, cognitive neurodynamic, and brain-computer interfaces (BCIs).
Non-Digital Computer Substrates: ESNs can use a variety of physical items as their nonlinear “reservoir,” such as optical microchips, mechanical nano-oscillators, polymer mixes, or prosthetic soft limbs, because they do not require parameter adjustment in the RNN.

Also Read About Spatial Transformer Networks Advantages and Key Properties

Challenges and Upcoming Projects

Even while ESNs are useful, deploying them correctly frequently calls for knowledge and experience. The stochastic nature of randomly seeded input and reservoir matrices makes hyper-parameter optimization a substantial issue that is not easily solved. The goal of research is to develop guidelines for this tuning in order to significantly accelerate optimization.

The study of ESNs will be expanded to other problem types and datasets in the future. It will also examine less well-known variations that concentrate on more complex topologies (such as neural hierarchies, sub-goal divided reservoirs, deep ESN, and next generation reservoir computing) and assess the impact of additional metrics like isometric properties. In order to obtain performance certificates, there is also interest in using reservoir computing as a data-driven lifting technique for time-series prediction.

Page Content

Tutorials