Implicit Matrix Factorization: What is it?
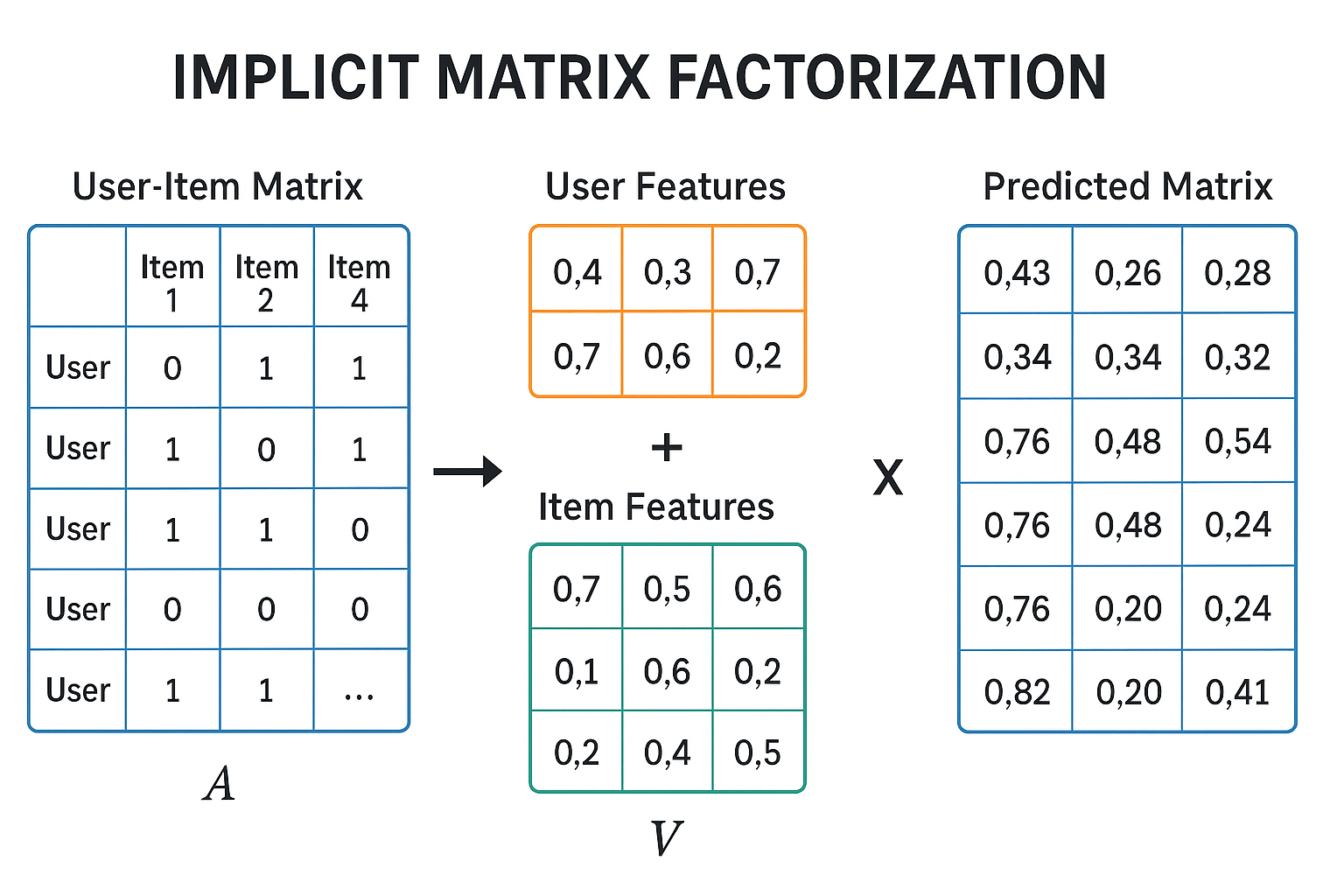
In a number of fields, such as natural language processing (NLP) and recommender systems, implicit matrix factorization can be used. Its principal objective is to reveal hidden structures or features in data that are deduced from indirect signals but not explicitly observed. In contrast to techniques that depend on explicit input, such as ratings, implicit matrix factorization makes use of feedback that is inferred from user interactions, such as clicks, views, or purchases.
Importance
When working with huge, sparse datasets that lack the majority of interactions, this method is quite helpful. It is an effective technique for personalization and suggestion since it enables systems to comprehend user preferences and item features even in the absence of explicit ratings. The acts a user does, like watching or purchasing, teach the system about their preferences.
Important Ideas:
Hidden variables deduced from observed data are known as latent factors. While latent factors can reflect user preferences and item qualities in recommendation systems, they can also represent abstract concepts or subjects that underlie word co-occurrences in natural language processing (NLP).
Co-occurrence Matrix: A matrix that shows how frequently words, users, and items occur together. A co-occurrence matrix in NLP may show how frequently word pairings occur together in a certain context.
The process of breaking down a huge matrix into the product of two smaller matrices is known as matrix factorization. The data’s fundamental structure is maintained while its dimensionality is decreased through factorization.
You can also read What is Matrix Factorization in Machine Learning?
Here is a summary of its main features and operation:
Presentation of Data:
The procedure frequently begins with a matrix that shows interactions or co-occurrences.
In lieu of explicit star ratings, this might be a user-item matrix in recommender systems, where a “1” denotes a user engaging with an item (watching a movie, for example) and a “0” denotes no interaction.
In NLP, this might be a word co-occurrence matrix that displays the frequency with which word pairings occur together in a certain context.
When working with huge, sparse datasets that lack the majority of interactions, this strategy is quite helpful.
Factorization:
The main concept is to split this interaction/co-occurrence matrix, which may be sparse and massive, into two lower-dimensional matrices.
These are usually a “user” matrix and a “item” matrix in recommender systems.
The underlying patterns or interactions between items, such words, would be captured by these matrices in natural language processing.
These lower-dimensional matrices stand for hidden traits or latent components. Latent factors can represent abstract notions or subjects that underlie word co-occurrences in natural language processing (NLP), and they can represent item qualities and user preferences in recommendation systems.
Forecasting/Comprehending Connections:
The matrices can be utilized for predictions after they have been factored. An estimated “preference” in a recommender system is obtained by taking the dot product of the corresponding user and item vectors. If users who interact with action films have a common latent factor, for instance, this factor can assist predict that other users who share that factor would also enjoy action films.
Finding latent semantic links between words or underlying subjects in documents is made possible in natural language processing (NLP) by factorizing a word co-occurrence matrix. For applications like sentiment analysis and machine translation, this aids in the creation of word embeddings that capture semantic commonalities.
Essential Ideas:
- Latent Factors: Unobserved variables that are hidden and represent ideas, subjects, inclinations, or characteristics.
- Implicit matrix factorization is ideally suited to handle sparse data, which are datasets in which the majority of possible interactions or co-occurrences are absent.
- Inferred Preferences: Identifying user preferences without direct input (ratings) by using behaviors (viewing, purchasing).
- A matrix that shows how frequently certain things (such as words, users, or items) occur together is called a co-occurrence matrix.
Applications
- Implicit matrix factorization is frequently used in recommender systems to make product recommendations based on previous user interactions.
- Identifying underlying subjects and learning the semantic links between words are two applications of natural language processing, or NLP.
NLP Implicit Matrix Factorization Methods:
Some methods are frequently employed to measure word associations in the context of implicit matrix factorization for natural language processing:
Pointwise Mutual Information (PMI):
Assesses the correlation between two occurrences (for example, two words occurring together) by comparing their joint probability to their individual probabilities.
Formula: PMI(x, y) = log (P(x, y) / (P(x) ⋅ P(y))).
Explanation:
- Strong associations are indicated by high PMI; words that happen to come together more frequently than they should by coincidence.
- When their PMI is zero, they happen together as frequently as would be predicted by chance.
- When the PMI is negative, they co-occur less frequently than anticipated.
Positive Pointwise Mutual Information (PPMI):
All negative PMI values are set to zero in this variation of the PMI.
Formula: PPMI(x, y) = max(PMI(x, y), 0).
Explanation:
The explanation is better appropriate for tasks like word embeddings and topic modelling since it only keeps positive PMI values and concentrates on significant and powerful positive word associations.
Shifted PMI:
A shift parameter (k) is introduced in order to normalize PMI measurements.
Formula: Shifted PMI(x, y) = PMI(x, y) – log(k).
Explanation:
By lessening the impact of exceptionally high PMI values for infrequent co-occurrences, it helps balance values and lessen the impact of rare word pairings.
All things considered, implicit matrix factorization is a potent technique that enables computers to comprehend user preferences, object attributes, or semantic word associations even in the absence of explicit ratings or direct observations. These associations are quantified and dense word representations are produced in NLP using techniques such as PMI, PPMI, and Shifted PMI.
