Recursion in DSA
A powerful programming method is recursion, in which a procedure or function describes itself in terms of itself. It is essentially a way to accomplish repetition in a computer program that provides an alternative to more conventional loops such as while or for structures. Functional recursion in DSA is supported by the majority of contemporary programming languages via the same mechanism as regular function calls.
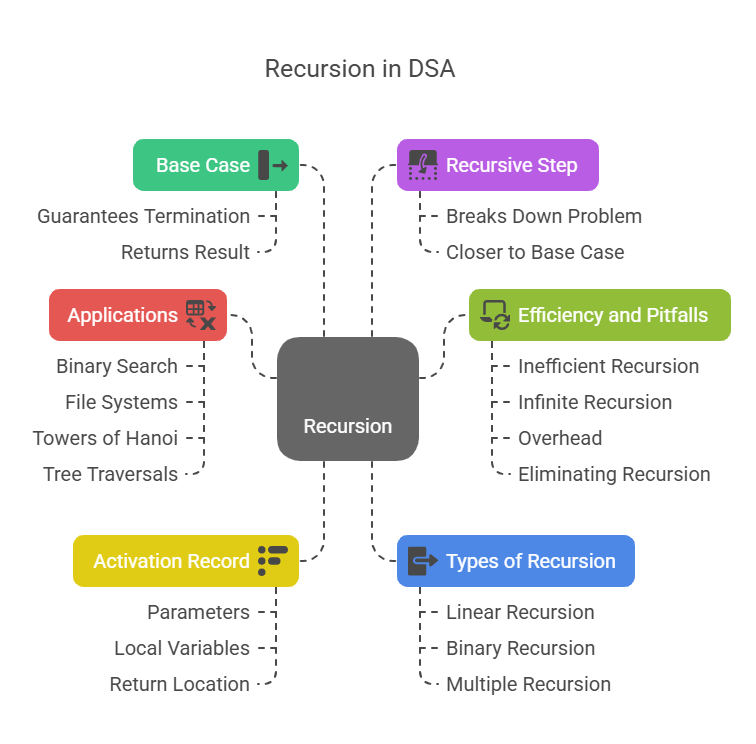
Key Characteristics of Recursive Routines:
Base Case: One or more base cases are required for a recursive algorithm. Under these circumstances, the function guarantees that the recursion in DSA eventually ends by returning a result without making any more recursive calls. Every conceivable sequence of recursive calls should eventually lead to one when the base cases are defined.
Recursive Step: The function makes one or more recursive calls if it isn’t a base case. In order to get closer to a base case, this stage usually entails breaking the problem down into a smaller instance of the same problem.
What’s Really Happening During Recursion?
A structure called an activation record or frame is produced when a recursive function is called. The parameters, local variables, and the location in the code where execution should restart following the completion of a nested call are among the crucial details about that particular invocation of the function that are stored in this record. A fresh activation record is added to the call stack each time a recursive call is made. Control moves back to the caller’s activation record when a function returns (for example, when it reaches a base case) and pops its activation record off the stack. This procedure permits the same function to be called more than once on the stack at once.
Illustrative Example: The Factorial Function
A Case in Point The Factorial Function As the product of integers from 1 to n (with 0! = 1), the factorial function (n!) is a well-known example of a problem having a naturally recursive definition.
This is an implementation in Python:
def factorial(n):
# Base case
if n == 0:
return 1
else:
# Recursive case
return n * factorial(n - 1)
# Test the function
number = 5
result = factorial(number)
print(f"The factorial of {number} is {result}")Output:
The factorial of 5 is 120In this function:
- If n is 0, basic case returns 1.
- Recursion occurs when factorial calls itself with a lesser parameter, n-1.
- The execution can be seen with the use of a recursion trace. Regarding factorial (5).
- Factorial (5) invokes factorial (4) through
- Calling factorial(3), factorial(4)
- Calling factorial(2), factorial(3)
- Calling factorial(1), factorial(2)
- Factual(1) invokes Factual(0)
- The basic case of factorial (0) is 1.
- Factorial(1) returns 1 for 1 * 1.
- With 1 input, factorial(2) produces 2.
- factorial(3) returns 6 after getting 2.
- Given 6, factorial(4) returns 24.
- Factorial(5) returns 120 after getting 24.
This function’s examination reveals that there are n+1 activations, each of which carries out a certain number of operations. Therefore, O(n) is the total running time for computing factorial(n).
Other Applications of Recursion
Recursion is extensively employed in many different data structures and algorithms. Among the noteworthy instances are:
Binary Search: An effective O(log n) time technique for locating a target value in a sorted sequence. It is a linear recursion example.
File Systems (Disc consumption Calculation): Recursive implementation provides a natural way to perform tasks like calculating the total disc consumption for directories, where directories can be nested. An illustration of multiple recursion in DSA is this.
Towers of Hanoi:The Towers of Hanoi puzzle is a famous recursion demonstration. The problem has a platform with three pegs (a, b, and c) and ‘n’ discs of various sizes, initially piled in decreasing order on one peg (such as peg ‘a’), with the smallest disc at the top. The goal of the puzzle is to move all the discs from the first peg to peg ‘c’. Two rules must be followed: only one disc can be moved at a time, and a larger disc cannot be placed on a smaller one
Tree Traversals: Recursive implementations are commonly used for algorithms such as in-order, pre-order, and post-order traversals of binary trees and generic trees. For example, recursion in DSA that takes the current depth as a parameter provides an efficient way to print trees with indentation in O(n) time.
Types of Recursion
Linear Recursion: When the function body makes no more than one new recursive call each invocation, this is known as linear recursion. Binary search, the good fibonacci function, and the factorial function are a few examples.
Binary Recursion: Binary recursion is the result of two recursive calls made by a function. Examples are the English ruler drawing function and the bad fibonacci function.
Multiple Recursion: When a function may make more than two recursive calls, this is known as multiple recursion. Examples include combinatorial problem solvers and file system disc space usage algorithms.
Efficiency and Pitfalls of Recursion: Recursion offers elegant solutions, but when used improperly, it can result in ineffectiveness or deadly mistakes.
Inefficient Recursion: Because of redundant computations, directly implementing some recursive definitions (such as bad fibonacci, which makes two recursive calls) might result in an exponential number of function calls and, thus, an exponential running time (e.g., O(2^n)). There is a serious risk associated with this “snowballing effect”. Restructuring the function to avoid recomputation and provide essential information between calls can make more efficient recursive algorithms (e.g., good fibonacci) attain linear time (O(n)).
Infinite Recursion: An infinite sequence of calls is formed if a recursive call never reaches a base case. Because call stack activation records use memory quickly, this is a major issue that can quickly exhaust computer . To avoid such problems, Python has a maximum recursion depth by default.
Overhead: In order to create and manage activation records, method calls including recursive ones incur overhead. In algorithms with high growth rates (e.g., O(n²), O(n³), or O(2^n)), this overhead might cause stack overflow or significantly slow down operations
Eliminating Recursion: Recursive algorithms are converted to iterative ones by eliminating recursion to reduce memory consumption and execution performance. Recursion requires the Python interpreter and other programming languages to keep an activation record or frame on the call stack for each nested function call. This overhead can cause memory use, stack overflow issues, and decreased performance in deep recursion or algorithms with high runtime complexity (e.g., O(n^2), O(n^3), or O(2^n)).
- Recursive call layering can be deliberately managed using the stack data structure (Last-In, First-Out principle), which emulates the call stack of the interpreter. By saving only the most important information, this could lower memory use.
- Tail recursion is a unique type of linear recursion in which the enclosing function returns the return value instantly and the recursive call is the final operation in its environment.
- By substituting a loop for the recursive call and reassigning parameters, tail recursions can be effectively reimplemented non-recursively, hence removing the need for auxiliary memory such as a stack. Sequence reversal and binary search are two examples.
