Sorting Techniques in DSA
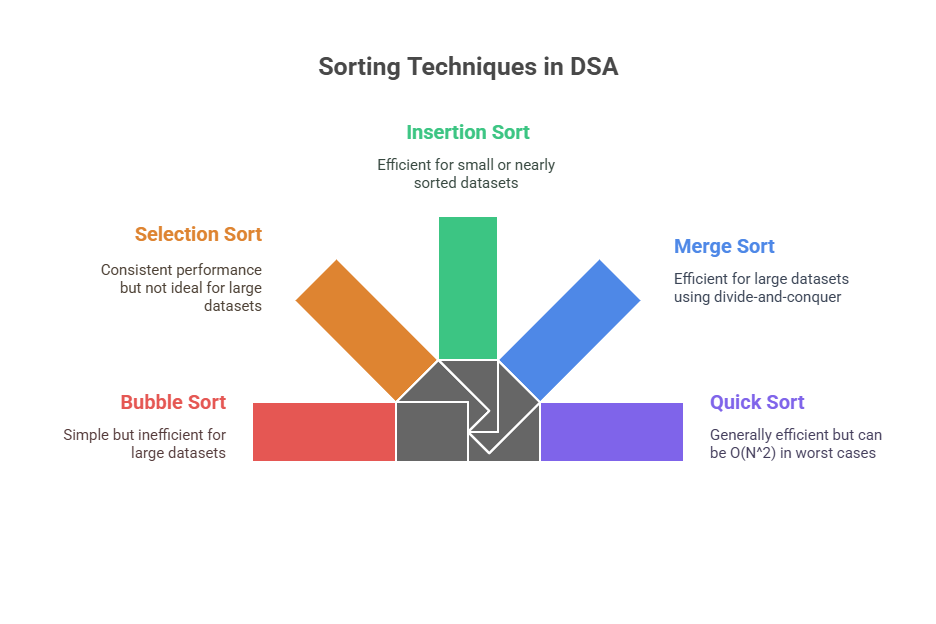
Comprehending sorting techniques is essential for contemporary computer engineers as it facilitates effective information organisation and retrieval. The mechanisms, effectiveness, and Python implementations of the several sorting algorithms will be the main topics of this part. Sorting means putting information in a certain order, usually lexicographical or numerical. Sorting is important since it makes it easier to search for data and presents it in more readable formats.
Besides introducing essential data structures that every programmers should know, “Data Structures & Algorithms in Python” explores how algorithms and data organisation affect computability . Python’s large libraries, object-oriented design, and user-friendliness make it attractive for implementing these ideas. Understanding Python’s efficient sorting algorithms is necessary. OOP is used to create all data structures as classes.
Discuss several sorting algorithms
Bubble Sort
A list is continuously stepped through using the straightforward but ineffective comparison-based algorithm known as “bubble sort,” which compares nearby items and swaps them if they are out of order. The list is sorted when no swaps are required, which is achieved by repeating this process. In the worst situation, it is O(N^2).
Example:
list1 = [78, 109, 111]
print("Unsorted list1 is", list1)
# Bubble Sort Algorithm
n = len(list1)
for j in range(n - 1):
for i in range(n - 1 - j):
if list1[i] > list1[i+1]:
list1[i], list1[i+1] = list1[i+1], list1[i]
print("Sorted list is", list1)Output:
Unsorted list1 is [78, 109, 111]
Sorted list is [78, 109, 111]Selection Sort
Finding the least element from the unsorted portion of an array and repeatedly placing it at the start of the sorted subarray is how selection sort sorts an array. The array is split up into a sorted and an unsorted subarray by the algorithm. The smallest element from the unsorted portion is chosen for each iteration and transferred to the sorted portion. At worst and at best, its efficiency is O(N^2).
Example:
def selection_sort(arr):
n = len(arr)
for i in range(n):
min_idx = i
for j in range(i+1, n):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]
arr = [64, 25, 12, 22, 11]
selection_sort(arr)
print("Sorted array:", arr)Output:
Sorted array: [11, 12, 22, 25, 64]Insertion Sort
The basic sorting method “insertion sort” moves each element into a developing sorted list segment. It’s like sorting cards. The approach sorts the first element first. Iterating over the remaining components shifts larger elements to the right to position them in the previously sorted subarray. Starting the array in reverse order produces a worst-case execution time of O(N^2). Almost or exactly sorted arrays take O(N) time.
Example:
def insertion_sort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i - 1
while j >= 0 and key < arr[j]:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
arr = [12, 11, 13, 5, 6]
insertion_sort(arr)
print("Sorted array:", arr)Output:
Sorted array: [5, 6, 11, 12, 13]Merge Sort
Quick Sort sorts well using divide-and-conquer. A “pivot” element is chosen from the array, and the remaining elements are divided into two size-based subarrays. Subarrays are then recursively sorted. Quick sort normally takes O(N log N) but can reach O(N^2) in severe circumstances. By choosing a solid pivot value, such median-of-three partitioning, worst-case scenarios can be avoided.
Example:
def merge_sort(arr):
if len(arr) > 1:
mid = len(arr) // 2
left = arr[:mid]
right = arr[mid:]
merge_sort(left)
merge_sort(right)
i = j = k = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
arr[k] = left[i]
i += 1
else:
arr[k] = right[j]
j += 1
k += 1
while i < len(left):
arr[k] = left[i]
i += 1
k += 1
while j < len(right):
arr[k] = right[j]
j += 1
k += 1
arr = [38, 27, 43, 3, 9, 82, 10]
merge_sort(arr)
print("Sorted array:", arr)Output:
Sorted array: [3, 9, 10, 27, 38, 43, 82]Quick Sort
The best sorting method relies on data type, operation frequency, and software maintenance. Quick Sort and Merge Sort are efficient for bigger datasets, however Insertion Sort is faster for smaller or almost sorted data. The Python built-in sort() method and sorted() function are efficient and sometimes use hybrid algorithms like Timsort (a mix of Insertion Sort and Merge Sort) for optimum results. Understanding these basic algorithms helps programmers arrange and process data.
Example:
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]
return quick_sort(left) + middle + quick_sort(right)
arr = [10, 7, 8, 9, 1, 5]
sorted_arr = quick_sort(arr)
print("Sorted array:", sorted_arr)Output:
Sorted array: [1, 5, 7, 8, 9, 10]Conclusion
In conclusion, a number of variables, such as the volume and kind of data, the frequency of operations, and software maintenance considerations, influence the choice of sorting algorithm. Simpler algorithms like Insertion Sort can operate more quickly on smaller or almost sorted data, while O(N log N) techniques like Merge Sort and Quick Sort are typically chosen for bigger datasets due to their efficiency.
For best results in a variety of situations, Python’s built-in sort() method and sorted() function are highly optimised and frequently employ hybrid strategies like Timsort, which combines Insertion Sort and Merge Sort. Comprehending these basic algorithms gives programmers a strong basis in computer science and empowers them to make well-informed choices regarding the processing and organisation of data.
