Types of Trees
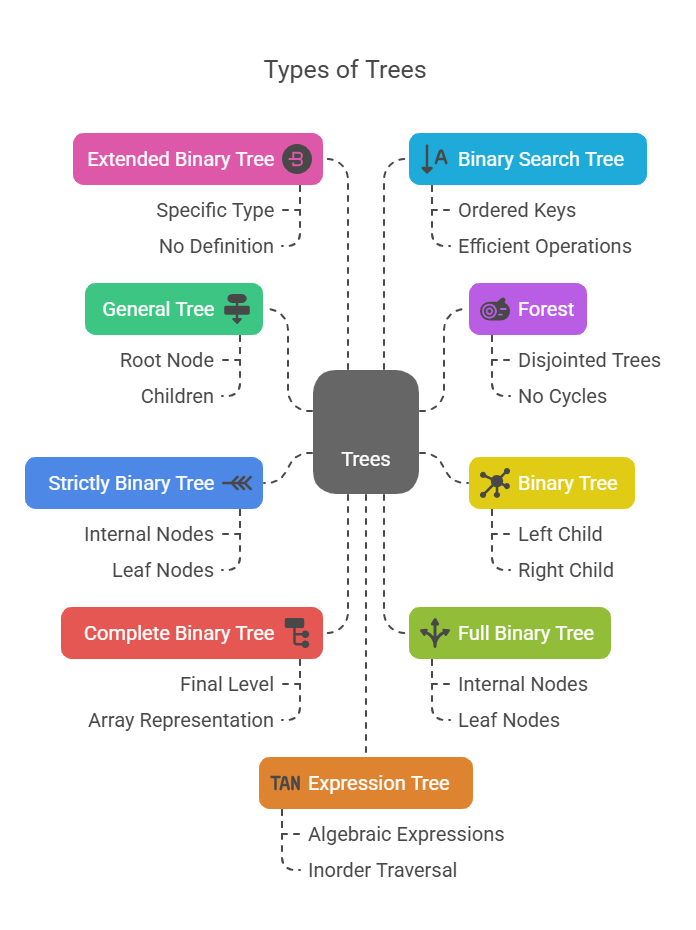
Trees are essential non-linear data structures that allow for hierarchical data organisation in computers and facilitate effective algorithms for a range of tasks. They are frequently found in file systems, databases, and graphical user interfaces and offer benefits over linear data structures like array-based lists or linked lists.
General Tree: An abstract data type known as a “general tree” is one in which all of the elements aside from the root, which is at the top have a parent and zero or more children. Computer applications frequently use nodes to represent entities like files or departments.In an object-oriented programming language, nodes are objects that represent these concepts.
There are no parents for the root, the top node. The parents of every other node are identical. There are two offspring per node in a binary tree, which is different from a generic tree. An example of a linked structure is a generic tree. Additionally, a general tree can be transformed into a binary tree.
Forest: A forest consists of at least one disjointed tree. A graph without any cycles is called a forest. Since a tree is essentially a connected forest that is, a connected graph devoid of cycles this idea fits within the broad category of trees. Trees are seen as a broader class of graphs.
Binary Tree: A binary tree is a specific type of tree in which there can be up to two offspring per node. Because of where they are when they are drawn, these two kids are explicitly referred to as the left and right children. In a binary tree, a node can have no children at all (i.e., it’s a leaf), only left children, or right children. The heights and number of nodes of binary trees are related; level d can have no more than 2^d nodes. It is possible to implement binary trees using an array-based representation or a linked structure.
Strictly Binary Tree: A strictly binary tree is one in which each non-leaf node has precisely two offspring. A strictly binary tree, often called a “proper binary tree” or “full binary tree”. Has nodes with zero or two children. All internal nodes in such a tree will have two children, while leaf nodes will have none. Defines a “full binary tree” as a binary tree with two children for every node except the leaves.
Complete Binary Tree: This type of binary tree has all nodes at the final level as far to the left as feasible and all levels possibly with the exception of the last are fully filled. By numbering the nodes and presuming that all are present to complete the binary tree, an array can be used to represent an incomplete binary tree.
Full Binary Tree: The number of children per node defines a full binary tree. Every node in a full binary tree must have two or zero offspring. This implies that entire binary trees contain two children for every internal nodes. Some call these “proper binary trees”. Half of a balanced full binary tree’s nodes will be on the bottom level, which has one more node than all subsequent levels.
Extended Binary Tree: Listed as a particular kind of binary tree is the Extended Binary Tree. The table of contents lists “Extended Binary Tree” as one of the tree types. In the portions that are provided,Do, not, however, define or explain what a “Extended Binary Tree” is in the sections that are specified.
Binary Search Tree (BST): Node keys are ordered in this binary tree. Right child of a node must have key larger than or equal to parent’s key, whereas left child must have key less. This distinguishes it. This order allows efficient node location, addition, and removal in O(log N) time when the tree is balanced. These operations may become O(N) if an imbalance occurs.
Expression Tree: An algebraic expression can be represented by a binary tree called an expression tree. An expression tree’s inorder traversal, for instance, visits locations in a sequence that corresponds to the expression’s standard form.
Python Building and Operational Procedures
Python may be used to construct and manipulate several of these tree types. The implementation of Binary Search Trees.
Constructing a Binary Search Tree (BST)
Nodes are arranged by their keys in a Binary Search Tree class, which usually starts empty. The constructor sets root node to None. An inner Node class with pointers to the node’s parent, left child, right child, and element is a typical approach to describe tree nodes.
Example:
# calculator.py
def add(a, b):
return a + b
def subtract(a, b):
return a - b
def multiply(a, b):
return a * b
def divide(a, b):
if b == 0:
raise ValueError("Cannot divide by zero.")
return a / b
def calculator():
print("Simple Calculator")
print("1: Add | 2: Subtract | 3: Multiply | 4: Divide")
try:
choice = int(input("Enter choice (1-4): "))
if choice not in [1, 2, 3, 4]:
raise ValueError("Invalid choice.")
a = float(input("Enter first number: "))
b = float(input("Enter second number: "))
operations = {1: add, 2: subtract, 3: multiply, 4: divide}
result = operations[choice](a, b)
print(f"Result: {result}")
except ValueError as ve:
print(f"Error: {ve}")
except Exception as e:
print(f"Unexpected error: {e}")
if __name__ == "__main__":
calculator()Output:
Simple Calculator
1: Add | 2: Subtract | 3: Multiply | 4: Divide
Enter choice (1-4): 3
Enter first number: 1
Enter second number: 3
Result: 3.0Together with pointers to its left and right children, the key and data would be contained in the Node class. For debugging, you can add its str() function to display contents without displaying child nodes.
Building an Expression Tree
It is possible to create an expression tree from a postfix expression. Although whole subtrees are kept on a stack rather than operands, the method is comparable to evaluating a postfix expression. Upon encountering an operand (variable or number), the stack is pushed with the trivial tree that contains that value. A new subtree with the operator as the root is created by combining two subtrees from the stack when an operator is found.
Example:
class ExpressionTreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class ExpressionTree:
def __init__(self):
self.root = None
def build_tree(self, postfix):
stack = []
for char in postfix:
if char.isdigit():
# Operand: Create a leaf node
stack.append(ExpressionTreeNode(char))
else:
# Operator: Pop two nodes and create a new tree
node = ExpressionTreeNode(char)
node.right = stack.pop()
node.left = stack.pop()
stack.append(node)
self.root = stack.pop()
def evaluate(self, node):
if node is None:
return 0
if node.value.isdigit():
return int(node.value)
left_val = self.evaluate(node.left)
right_val = self.evaluate(node.right)
return eval(f"{left_val} {node.value} {right_val}")
def inorder(self, node):
if node:
self.inorder(node.left)
print(node.value, end=" ")
self.inorder(node.right)
# Example Usage
expression = "34+52-*"
tree = ExpressionTree()
tree.build_tree(expression)
print("Inorder Traversal of Expression Tree:")
tree.inorder(tree.root)
print("\nResult of Expression Evaluation:")
print(tree.evaluate(tree.root))Output:
Inorder Traversal of Expression Tree:
3 + 4 * 5 - 2
Result of Expression Evaluation:
21This illustrates how Python implements and uses various tree architectures, striking a balance between academic knowledge and real-world application.
