What is a deep belief networks? and its Advantages

What is a deep belief networks?

One kind of generative deep learning model composed of several layers of random, latent variables is called a Deep Belief Network (DBN). Restricted Boltzmann Machines (RBMs), a type of neural network that can learn to represent probability distributions over inputs, typically make up these layers. Advanced machine learning models known as Deep Belief Networks (DBNs) have been crucial to the development of deep learning.

Composition

Several simpler, unsupervised networks, most frequently Restricted Boltzmann Machines (RBMs), are stacked to build DBNs. One sub-network’s hidden layer is the next one’s visible layer.

Design

These feedforward neural networks feature a deep design, which means that there are a lot of hidden layers. Units inside a single layer are not connected. While layers below them have directed links to lower layers, the top two layers are directionless and create associative memory.

Stochastic Latent Variables

Also known as feature detectors or hidden units, DBNs are made up of multiple layers of stochastic (randomly determined) latent variables.

Hybrid Generative Graphical Model

One type of generative graphical model that is regarded as hybrid is the DBN. When trained without supervision, they can recreate their inputs probabilistically.

DBNs were created to solve problems with traditional neural networks in deep layered networks, including their slow learning, tendency to become trapped in local minima as a result of subpar parameter selection, and need for a lot of training data.

History of Deep Belief Networks

The first generation of perceptrons, which were used to identify objects based on weight, marked the beginning of the evolution of neural networks. Perceptrons, however, were restricted to simple technology. Backpropagation, which compares received and desired outputs, was developed by the Second Generation of Neural Networks to lower error values. After that, belief networks directed acyclic graphs arose to address learning and inference issues.

Geoffrey Hinton et al. first presented Deep Belief Networks in 2006. One of the earliest successful deep learning algorithms was Hinton’s invention, which involved the greedy, layer-by-layer training of these deep networks. DBNs were essential to the development and expansion of deep learning.

How DBNs Work

The two main stages of DBN operation are pre-training and fine-tuning.

Unsupervised learning, or pre-training

• The goal of this first stage is to set the DBN’s weights to accurately reflect the incoming data.
• A greedy learning algorithm is employed. A layer-by-layer method is used to train each RBM layer separately and one at a time.
• The learning models are gradually improved by using the output from a previously trained RBM as the input for the subsequent one.
• RBMs assist the network in comprehending the underlying data structure by learning the inputs’ probability distribution.
• The Contrastive Divergence (CD) algorithm is commonly used for training individual RBMs. Through the computation of probabilities of hidden layer states from visible units, CD consists of a positive phase that increases the likelihood of the training data and a negative phase that decreases the likelihood that the model will generate samples. The RBM learns accurate representations of the incoming data to this approach.
• Every RBM in a DBN is an energy-based model; a higher likelihood of association between units is indicated by a lower energy value. The RBM creates a credible depiction of the original data by reducing this energy.

Also Read About What is an Echo State Networks? and Advantages of ESNs

Supervised learning, or fine-tuning

• Following pre-training, the parameters of the DBN are modified for a particular task, such regression or classification.
• In this stage, supervised learning algorithms such as backpropagation are frequently used. The performance of the network is assessed, and parameters are updated based on errors.
• Training proceeds more quickly and produces better results during the fine-tuning phase when the pre-training weights are used.

DBN architecture

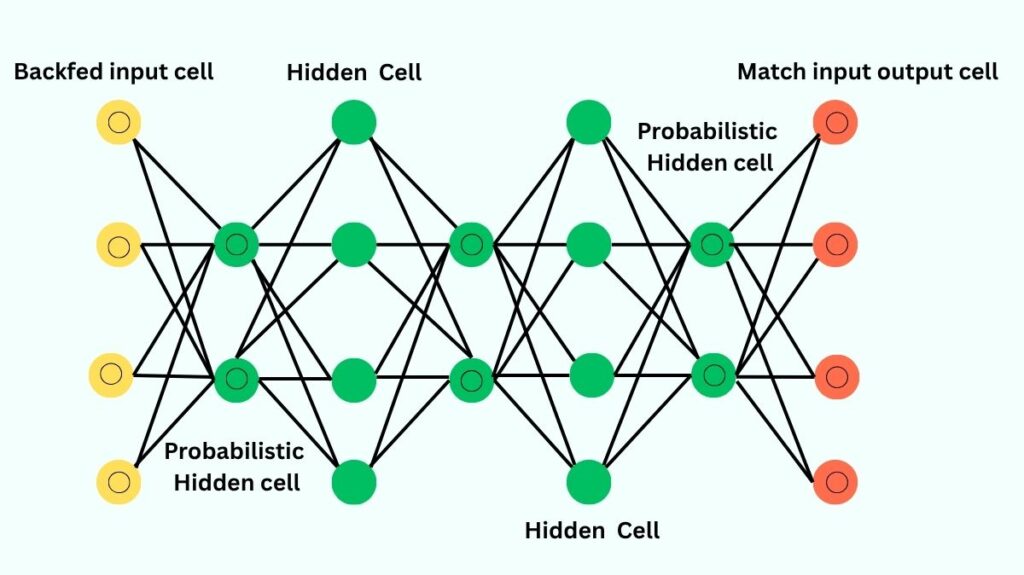
A sequence of Restricted Boltzmann Machines (RBMs) is stacked in a certain order to create a Deep Belief Network.

• Layer Connections: The output of one Boltzmann machine’s “output” layer is used as the successive input to the subsequent one.
• Connections Within Layers: It is important to note that DBNs do not have connections between units within a single layer.
• Top Layers: A DBN’s top two layers form associative memory through symmetric, undirected connections.
• Lower Layers: Arrows pointing to the layer nearest the data show the relationships between all lower layers. Associative memory is converted to observable variables by directed acyclic connections in the lower layers.
• Input Layer: The visible units that make up the lowest layer receive input data, which may be actual or binary data.
• Dual Role of levels: Every layer in a DBN, with the exception of the first and last levels, has two purposes: it is the input layer for the nodes that come after it and it is the hidden layer for the nodes that come before it.
• CDBN: A Classification DBN (CDBN) is a particular kind of classification model with a CRBM record as its top-level associative memory. This makes it possible to train the top layer to identify unknown data vectors and provide class labels.

Features of DBNs

• Hybrid Learning Capabilities: DBNs are flexible enough to do both supervised learning (for tasks like classification or regression) and unsupervised learning (for feature learning, dimensionality reduction, and generative modelling).
• Deep Architecture: They have several hidden layers that, over time, provide a sophisticated comprehension of the input. Higher levels recognise more abstract concepts, while lower layers identify simple patterns.
• Feature Extraction: They are excellent at learning internal feature representations, extracting various features from input data, and serving as a nonlinear dimensionality reduction technique.
• Hierarchical Representation: Data representation is a skill that DBNs acquire.
• Probabilistic Nature: They can investigate and discover intricate patterns because they employ stochastic units that make decisions in a probabilistic manner.
• Effective Training Mechanism: RBMs’ greedy layer-wise training streamlines the deep representation training procedure.

Benefits of DBNs

Compared to other deep learning models and traditional neural networks, deep belief networks have the following advantages:

• Computational Efficiency: Unlike feedforward neural networks, which develop exponentially with the number of layers, they are less computationally expensive, with computational complexity increasing linearly.
• Vanishing Gradients: The issue of vanishing gradients is less likely to affect DBNs.
• Quicker Training and Better Outcomes: DBNs can accomplish quicker training and better outcomes because of their efficient weight initialisation during pre-training. Achieving global minima is aided by this initialisation.
• Managing Big Data: By employing hidden units to uncover underlying relationships, they are able to manage big datasets.
• Their ability to learn abstract features that are resilient to noise and transformation is known as robust feature learning.
• Adaptability: By learning to produce data and labels at the same time, they can be modified to solve supervised tasks.
• High Accuracy: DBNs have demonstrated more efficacy and accuracy in some defect detection applications when compared to other machine learning methods such as MLP and SVM, particularly when used on denoised data.

Drawbacks of Deep Belief Networks

DBNs provide benefits, but there are drawbacks as well:

• Data Requirements for Probabilistic Models: Because DBNs are probabilistic, they frequently need a lot of data in order for the model to accurately identify underlying patterns.
• Complexity in RBM Training: RBMs make DBN training easier, but they can still be challenging to train because they may need a lot of hidden units to approximate any distribution.
• Performance Problems in Implementations: A DBN for digit classification produced a low accuracy score (around 21.14%) and an unexpected trend in pseudo-likelihood values in one example implementation, indicating that efficient training can be difficult and parameter-sensitive. This shows that training or data processing may need to be changed for better outcomes.
• Due to developments in standard deep networks like CNNs and RNNs, DBNs are losing popularity in computer vision and natural language processing applications, despite their historical importance.

Deep Belief Networks applications

DBNs can be used for activities that involve a variety of data kinds and huge datasets. Among their uses are:

• Image Recognition and Classification: For example, recognising tumours in medical scans or handwritten numbers.
• Speech Recognition.
• Motion Capture Data and Video Sequences (mocap).
• Dimensionality reduction and feature learning: learning hierarchical representations and simplifying data.
• Generative Modelling: The capacity to produce fresh data samples and comprehend latent data representations.
• Filtering through collaboration.
• The discovery of human emotions.
• Time Series Prediction: This includes financial forecasting, wind forecasting, and forecasting for sustainable power sources.
• The diagnosis of cancer.
• Monitoring of Machine Health.
• Defect Detection: By examining acoustic signals or images, this technique is used in manufacturing processes such as metal laser-based additive manufacturing.
• Estimating the battery’s state of charge (SOC).
• Human Activity Recognition: Employing wearable sensors to fuse data from many sensors.
• The discovery of drugs.

Additional Details

• DBNs vs. MLPs: DBNs function similarly to conventional multi-layer perceptrons (MLPs), but they have advantages such as improved weight initialisation and quicker training.
• Methods of Training: A successful DBN training program includes:
  • Greedy Layer-wise Training: RBMs are trained one at a time, with each new RBM being trained using the output of the previous one. A popular approach for training RBMs, Contrastive Divergence uses both positive and negative phases to learn data representations.
  • Learning Rate Selection: For the best learning results, it is essential to try out various rates. The Supervised Learning Algorithm fine-tunes the entire network for certain tasks by employing techniques like as backpropagation.
  • Regularisation Techniques: To avoid overfitting and guarantee generalisation to fresh data, techniques such as weight decay and dropout are used during fine-tuning.
• Python Implementation: Libraries such as numpy, pandas, scikit-learn, and tensorflow are frequently used while implementing DBNs. One example is developing a model on a dataset using Supervised DBN Classification, separating the data for testing and training, and assessing accuracy.