The ECC blockchain, its history, mathematical underpinnings, concepts, ECC algorithms, applications, RSA vs ECC, advantages, and disadvantages of elliptic curve cryptographyare all covered in this article.
ECC blockchain
A contemporary public-key cryptosystem called Elliptic Curve Cryptography (ECC) uses the algebraic structure of elliptic curves over finite fields to facilitate safe communication. Because of its effectiveness and robust security with reduced key sizes, it is seen as RSA’s logical modern successor.
Also Read About What Is ECDSA? Elliptic Curve Digital Signature Algorithm
History of elliptic curve cryptography
Neal Koblitz and Victor S. Miller independently proposed elliptic curve encryption in 1985. The ECC methods became widely used in 2004 and 2005. The suggested elliptic curve domain parameters, often known as “standard curves” or “named curves,” for cryptographic applications have been published by a number of standards groups, including NIST, SECG, and Brainpool.
Core Concepts and Mathematical Foundation
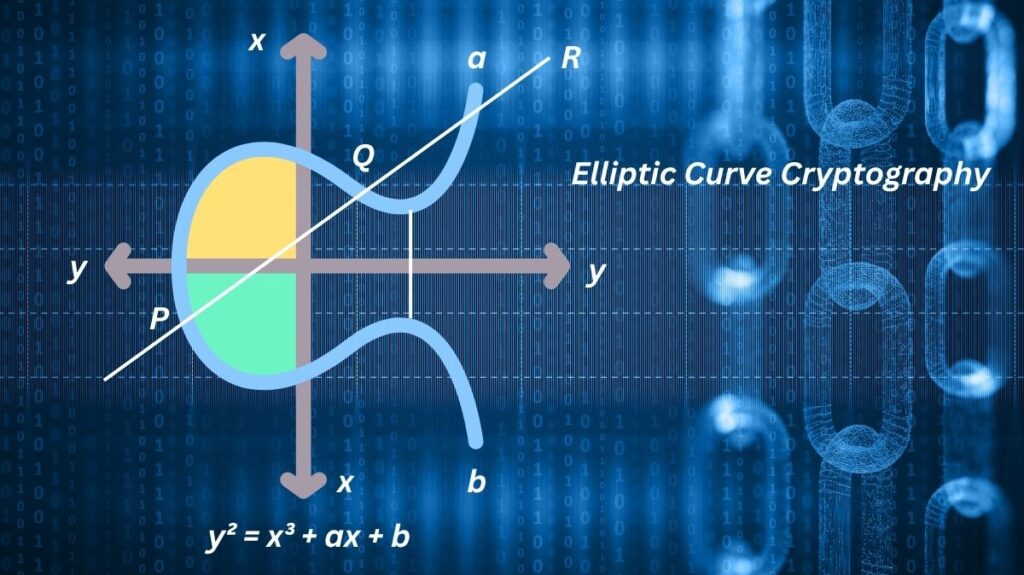
Fundamentally, ECC makes use of elliptic curves’ mathematical characteristics. A planar curve with points {x, y} that fulfil a particular equation usually in the Weierstrass form: y² = x³ + ax + b is called an elliptic curve. The particular curve is defined by the constants ‘a’ and ‘b’. These curves in cryptography are defined over finite fields (e.g., 𝔽2m where the field size is 2m or 𝔽p where ‘p’ is a huge prime number). This results in a square matrix of size p x p, where the points on the curve are restricted to integer coordinates within a given range.
Among the crucial mathematical processes in ECC are:
- Point addition is the process of finding a third point, R, such that P + Q = R, given two points, P and Q, on an elliptic curve.
- Point Doubling: G + G = 2G is the outcome of adding a point G to itself. It is possible to repeat this technique.
- Scalar Multiplication: Another EC point P on the same curve can be obtained by multiplying an EC point G by an integer k (P = k * G). This process is quick. This process is essential to the creation of ECC keys.
Also Read About Features, Advantages Of Symmetric Cryptography In Blockchain
Key Concepts in ECC
- Public and Private Keys: ECC employs a pair of linked keys, a public key and a private key (secret), just like other asymmetric cryptosystems.
- The process of creating a private key is fairly rapid and involves nothing more complicated than safely producing a random integer within a predetermined range. A valid ECC private key is represented by any integer in the field.
- EC points, or pairs of integer coordinates {x, y} that lie on the curve, are the public keys. A generator point (G) is multiplied with the private key to determine the public key.
- Generator Point (G): The generator point G, sometimes referred to as the base point, is a unique pre-determined EC point that is defined by ECC cryptosystems. By multiplying G from an integer, this point can produce any other point in its subgroup over the elliptic curve. Cryptographers optimise for performance by carefully choosing this moment to generate the complete group or a subgroup. The entire number of potential private keys for the curve is determined by the order (r) of this cyclic subgroup.
- Discrete Logarithm Problem with Elliptic Curves (ECDLP): The computational difficulty of the ECDLP determines the security of ECC. It is computationally impossible to determine the integer ‘k’ such that P = k * G given an elliptic curve, a generator point G, and another point P on the curve. P = k * G can be calculated relatively quickly, but the converse operation finding k given P and G is very difficult and impossible for big ‘k’. The foundation of ECC’s security strength is this asymmetry.
ECC Algorithms
ECC offers a number of algorithm groups that are based on elliptic curve arithmetic over finite fields:
Digital Signature Algorithms
- Digital signatures are the main application for the sophisticated public-key cryptography system known as the Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA is used by Ethereum and Bitcoin to sign transactions.
- As a quicker substitute for ECDSA, the Edwards-curve Digital Signature Algorithm (EdDSA) is suggested because it offers better performance and easier, safer embedded device implementations. Ed448 and Ed25519 are two examples.
Encryption Algorithms
- The Elliptic Curve Integrated Encryption Scheme (ECIES) is a public-key authenticated encryption method that creates symmetric encryption keys from an ECDH shared secret using a key-derivation function (KDF). It is utilized in standards such as Intelligent Transportation Systems and can encrypt any volume of data. ECIES is used by Ethereum’s RLPx transport protocol for key exchange and handshaking.
- The public-key counterpart of ElGamal encryption techniques that makes use of the ECDLP is called EC-based ElGamal Elliptic Curve Cryptography.
Key Agreement Algorithms
- Elliptic curve Diffie–Hellman (ECDH): A key agreement protocol that uses public-private key pairs to enable two parties to establish a shared secret over an unprotected channel. A symmetric-key cypher can then be used to encrypt further communications using this shared secret.
- ECDH functions X25519 and X448 are obtained from particular Edwards curves.
- Adaptable to elliptic curve groups (ECMQV), Fully Hashed Menezes-Qu-Vanstone (FHMQV) is an authenticated key agreement mechanism built on the Diffie-Hellman technique.
Elliptic Curve Cryptography Applications
ECC’s effectiveness and robust security make it popular in a variety of fields:
- Blockchain technology is essential to the security of various cryptocurrencies, such as Ethereum and Bitcoin, mainly for digital signatures (ECDSA), which provide sender ownership and transaction authorisation. Shorter, alphanumeric addresses can likewise be derived from public keys using this method.
- Secure Communication: SSH and TLS use it to exchange digital certificates and keys. It can also encrypt emails with Pretty Good Privacy.
- Online Applications: Chat messaging apps, online banking, and online payments are using it increasingly due to its efficiency and smaller key size.
- Resource-Constrained Devices: Mobile devices, embedded platforms, and Internet of Things applications with limited processing and storage benefit from its effectiveness.
RSA vs ECC
ECC is sometimes contrasted with RSA, another popular public-key technique. The main distinctions are as follows:
Working Algorithm
ECC depends on the ECDLP’s difficulty and the algebraic structure of elliptic curves. The prime factorisation issue, which involves multiplying two huge prime integers to produce a public key, is the main foundation of RSA.
Security Strength
ECC is considered more secure than RSA for a given key size. A 3072-bit RSA public key is as secure as a 256-bit ECC key. Factoring big numbers is much easier than solving the ECC-based problem (ECDLP).
Key Size
To attain the same level of security as RSA, ECC utilises much smaller keys. Therefore, less transmission and storage are needed.
Efficiency
ECC creates keys, digital signatures, and key agreements faster than RSA. RSA decrypts faster than ECC. Devices with limited CPU and memory resources benefit most from this efficiency.
Elliptic curve cryptography advantages
- Smaller Key Size: Requires less storage and transmission space because it offers similar security with significantly shorter keys.
- Quick Key Generation: It’s really quick and as easy as safely creating a random integer.
- Reduced Processing Power: Encryption and decryption use less processing power when keys are shorter.
- High Security: Because the ECDLP is inherently challenging, it provides great security.
- Two-step signature computation reduces delay.
- Capable of encryption, key exchange, digital signatures, and pseudo-random number generation.
Also Read About Understanding Cryptography Mechanisms In The Blockchain
Disadvantages of elliptic curve cryptography
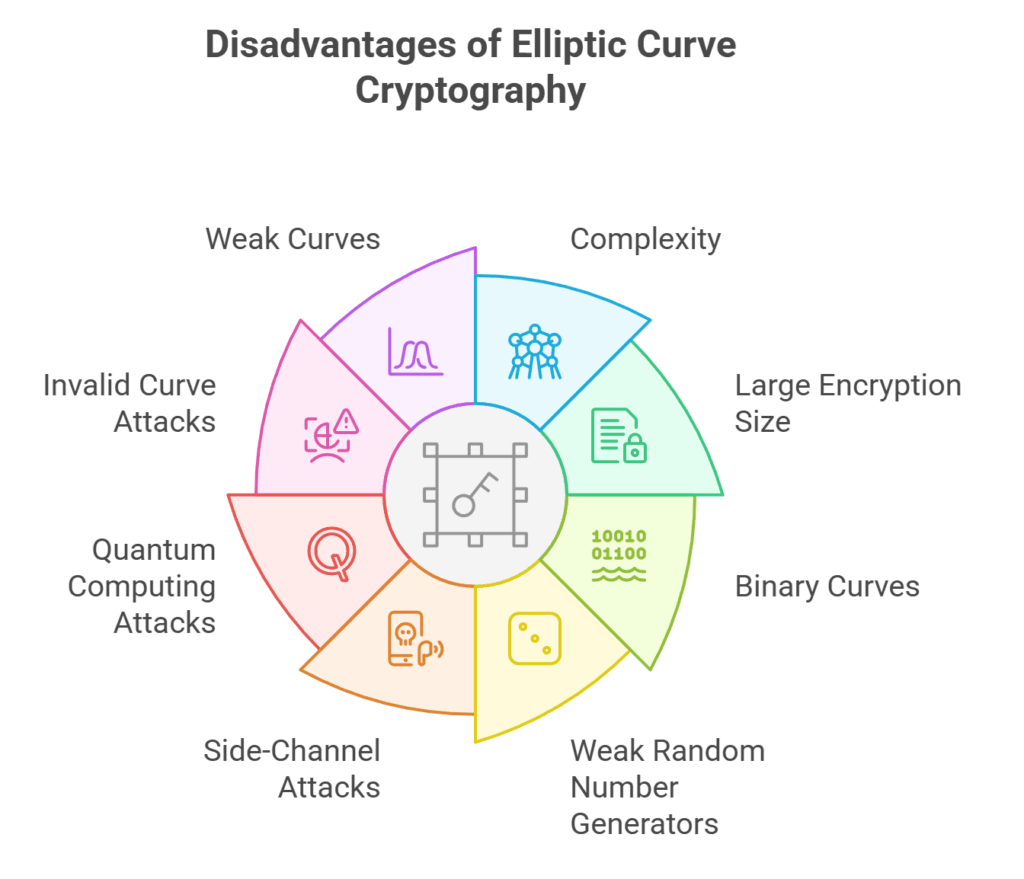
Complexity
ECC is more complicated and harder to implement properly than RSA. Implementing standard curves safely is particularly challenging.
Large Encryption Size
Compared to RSA encryption, ECC has a far greater capacity to enlarge the encrypted message.
Binary Curves
Binary curve processing can be expensive.
Weak Random Number Generators
A compromised random number generator can leak the private key. Concerns exist that the NSA inserted a kleptographic backdoor into the Dual Elliptic Curve Deterministic Random Bit Generator (Dual_EC_DRBG).
Side-Channel Attacks
ECC implementations may be vulnerable to side-channel attacks like timing or power analysis since they differ from addition and point doubling operations.
Quantum Computing Attacks
By computing discrete logarithms, Shor’s method may violate ECC if it were put into practice on a fictitious quantum computer. This is a problem for encryption in the future, even if it is currently outside the capabilities of contemporary quantum computers.
Invalid Curve Attacks
To get a complete Diffie-Hellman private key in virtual machine environments, an attacker may employ an invalid curve.
Weak Curves
Curves with non-prime’m’ over 𝔽2m or curves where the subgroup order ‘n’ divides p^B-1 for a small ‘B’ are examples of weak curves that should be avoided. The “named curves” (e.g., secp256k1, Curve25519) that are deemed secure and well researched are carefully selected and examined by cryptographers. Instead of making their own curves, developers are highly encouraged to adopt these well-established, standard curves.
