This Gives an overview of Disadvantages of Zero Knowledge Proofs, How it works, applications and examples.
Zero-Knowledge Proofs (ZKPs)
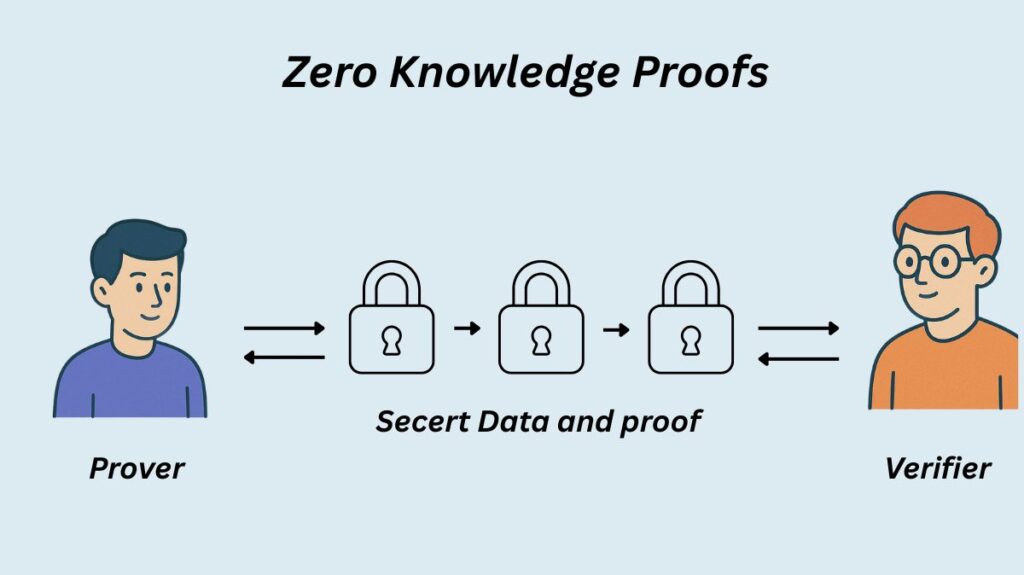
Zero-Knowledge Proofs (ZKPs) are a novel cryptographic technique that enables one party to demonstrate to another that a statement is true without disclosing any information beyond the statement’s veracity. This notion was a major advancement in cryptography and was first put forth in a 1985 scholarly work titled “The Knowledge Complexity of Interactive Proof Systems” by scholars Shafi Goldwasser, Silvio Micali, and Charles Rackoff. ZKPs, which improve user security and privacy, are now an essential part of many blockchains some 40 years later.
Core Properties of Zero-Knowledge Proofs
A ZKP interaction needs to meet three essential requirements in order to be deemed valid and effective:
Completeness: With a high likelihood, an honest prover should be able to persuade an honest verifier that the statement is true.
Soundness: The likelihood of a dishonest prover fooling an honest verifier into thinking a statement is true should be extremely low if it is false. This feature guarantees that the prover cannot manipulate the system.
Zero-Knowledge: Only the contents of the statements are disclosed to each side; neither can glean any more personal information about the other. In the event that the assertion is true, the verifier just gains knowledge of its truth.
How Zero Knowledge Proofs Work
ZKPs need two or more parties. the prover, who presents the verifier with the mathematical evidence to support their position, and the verifier, who considers the evidence and decides whether to accept or reject it. The verifier essentially requests the prover to carry out a sequence of activities that are only possible if the prover is aware of the underlying data. It is highly likely that the prover will be proven incorrect in the end if they are only speculating.
Several communication rounds between the prover and verifier are frequently used in the process to lessen the possibility of erroneous information or guesswork. As they establish mutual trust with provers, ZKPs, for example, use cryptographic hash functions to create random challenges for verifiers.
Zero-knowledge is defined more formally as a simulator that can generate a transcript that “looks like” an exchange between an honest prover and the verifier if it is simply given the assertion to be verified. This simulation feature guarantees that the verifier only discovers the statement’s veracity.
Zero Knowledge Proofs Examples
In order to better understand ZKPs, the following abstract examples are frequently used:
The Colour-Blind Friend and Two Balls: With two balls one red and one green Sachin (prover) must demonstrate to Sanchita (verifier), who is colour-blind, that they are different colours without identifying which is which. Sanchita asks Sachin if they were switched after repeatedly switching the balls behind her back. Since Sanchita is unable to identify the balls apart and Sachin is always right, she grows to believe that they are different colours without ever knowing whether is green or red.
Finding Waldo: The prover, Sachin, is aware of Waldo’s location on a page, but he chooses not to tell the verifier, Sanchita, where he is. By placing a large black board with a small hole the size of Wally over the page, Sachin allows Sanchita to see Wally without having to see where he is on the entire page. This exemplifies proving knowledge without disclosing the particulars.
The Ali Baba’s Cave: There are two entrances, A and B, to a ring-shaped cave, and Peggy (prover) says she has the secret word to open a magic door. The verifier, Victor, waits outside while Peggy enters and selects either path (A or B). After that, Victor calls out a path (A or B) at random for Peggy to leave. Peggy can always open the door if needed and leave along the designated path if she knows the word. She would have a 50% chance of making an accurate guess each time if she didn’t know the word. Through repeated use, Victor comes to believe that Peggy is familiar with the word even if she has never learnt it.
Types of Zero Knowledge Proofs
Interactive and non-interactive are the two main types of ZKPs.
Interactive ZKPs: These require the prover and the verifier to communicate back and forth several times. The prover replies with a solution after the verifier provides a challenge and the prover sends a commitment. Because they require both parties to be online at the same time, interactive proofs are often inefficient and rare in blockchain-based systems, despite their historical significance.
Non-Interactive ZKPs: These just require a single communication round in which the prover sends a single message to the verifier; concurrent online presence is not required. This is accomplished by the use of protocol primitives such as the Fiat–Shamir heuristic, which ensures unpredictability by substituting a hash function for the verifier’s challenge. Non-interactive ZKPs were first proposed in 1988.
Several types of non-interactive ZKPs are used in practice:
Zero-Knowledge Succinct Non-Interactive Arguments of Knowledge (zk-SNARKs): Since their introduction in 2012, zk-SNARKs have allowed players to demonstrate their possession of specific knowledge without disclosing specifics. Their conciseness (short proof size) and speedy verification periods define them. In Zk-SNARKs, elliptic curves are used. One major complaint is the requirement for an initial trusted setup, which could compromise security and be hard to find if compromised. The Ethereum blockchain frequently uses them for privacy-preserving Smart Contract, and Zcash uses them for shielded transactions, which hide sender, recipient, and amount information.
Zero-Knowledge Scalable Transparent Arguments of Knowledge (zk-STARKs): Designed to scale huge calculations, zk-STARKs, which were introduced in 2018, work similarly to zk-SNARKs. They are compatible with a variety of blockchain applications due to their post-quantum resistance and transparency (no trusted setup is needed, utilizing a publicly verifiable approach). They are not based on elliptic curves, but on information theory and hash functions. Their biggest drawback is that they have a bigger proof size than zk-SNARKs.
Bulletproofs: These ZKPs are brief and don’t require any trustworthy setup. They mostly demonstrate that a value falls inside a given range without actually disclosing the value. By using sophisticated mathematical ideas, bulletproofs reduce the size of proofs, which lowers transaction sizes and verification times. In Monero, bulletproofs are used.
PLONK: PLONK, which stands for “permutations over Lagrange-bases for oecumenical noninteractive arguments of knowledge,” employs a generic, reliable configuration that works with any software and can accommodate a large number of participants.
Technical Aspects of ZKPs
Sophisticated mathematical ideas and cryptographic techniques are necessary for ZKP implementation.
Elliptic Curves: In order to enable effective implementation of elliptic curve signature schemes within algebraic circuits, SNARK development leverages the finite, cyclic group nature of elliptic curves, which are geometric structures that are essential to cryptography.
Finite Fields: These algebraic structures serve as the basis for cryptographic protocols, facilitating effective arithmetic operations that are essential for security and computation. Because finite fields only allow finite sets of values, they make cryptographic processes simpler.
Secure Hash Functions: They convert arbitrary-sized data into fixed-size values (digests or hashes). The preimage-resistance, collision-resistance, and diffusion qualities of cryptographic hash functions like SHA256 are essential for the security and efficacy of ZKPs since they transform data while maintaining its integrity and confidentiality.
Zero Knowledge Proof Use Cases
With their many uses both inside and outside of the blockchain ecosystem, zero-knowledge proofs improve efficiency, security, and privacy.
Privacy-Preserving Transactions: ZKPs allow blockchain nodes to verify transactions without gaining access to private information, hiding from observers sender/recipient addresses, amounts, and smart contract code. ZKPs are used in cryptocurrencies such as Monero and Zcash for this reason.
Secure and Scalable Layer-2 Rollups: ZKPs package transactions off-chain and publish cryptographic proofs of their validity onto the mainnet, like Ethereum, in layer-2 scaling solutions (e.g., zk-rollups, Zk-Plasma, Validiums, Volitions). Compared to existing layer-2 solutions, this delivers faster finality, more throughput, reduced transaction costs, and a significant reduction in computing effort. Scroll, Polygon zkEVM, Starknet, Loopring, and ZkSync are a few examples.
Authentication and Secure Identity Verification: ZKPs enable people to demonstrate that they have particular qualities (such as citizenship, age, or group membership) or that they are aware of a secret (such as a password) without disclosing the sensitive personal data that lies beneath. In addition to helping organisations adhere to privacy laws like GDPR and HIPAA, this offers customers greater control over their data and guards against identity theft.
Secure Voting Systems: With ZKPs, individuals can demonstrate their eligibility to vote and their vote total without disclosing their background or personal preferences. Enhancing the system’s integrity, they also enable voters to independently confirm that their vote was recorded accurately without disclosing their selection.
Internet of Things (IoT) Security: ZKPs can provide secure communication between devices, confirm that only authorized devices are accessing a network or data, and check software upgrades. The energy efficiency of IoT devices can also be enhanced by lowering data transfer.
Supply Chain Transparency and Integrity Verification: ZKPs are able to verify suppliers’ qualifications and the legitimacy of products without giving up confidential information or transactional details to unapproved parties. Additionally, they can aid in confirming adherence to legal requirements.
Verifiable Computations: In the case of undercollateralized loans based on creditworthiness, for instance, ZKPs can be used by decentralised oracle networks to validate facts about off-chain data points without disclosing the underlying data on-chain. This is done without disclosing the precise score. The DECO technology from Chainlink is an illustration of an Oracle solution that uses ZKPs to protect privacy.
Decentralized Exchange: Trading a wide range of assets can be made easier by ZKPs without disclosing users’ account balances, trading histories, or methods.
Disadvantages of Zero Knowledge Proofs
Widespread ZKP implementation is fraught with difficulties, despite its potential:
Technical Complexity: Most developers lack a thorough understanding of sophisticated mathematics and cryptographic principles, which are necessary for implementing and deploying ZKPs.
Computational Resources: Large amounts of processing power are frequently required to generate ZKPs, which results in longer transaction processing times and more expensive fees.
Interoperability: Distinct ZKP protocols and verification techniques may provide challenges to blockchain interoperability.
Regulatory Compliance and Auditing: Regulatory compliance and auditing may be complicated by ZKPs’ intricacy and data storage features.
Furthermore, complicated security flaws, especially logic errors in their arithmetic circuits, can affect ZKPs. Under-constrained and non-deterministic circuits, arithmetic over/under flows, mismatched bit lengths, and defects in Fiat-Shamir implementations are typical problems. When necessary, trusted setups can also provide logistical and security problems if not managed properly. A thorough security audit is advised for any system that uses zero-knowledge.
With growing security and privacy consciousness propelling adoption, ZKPs on blockchain have a bright future. In order to promote interoperability, they are anticipated to be crucial in enhancing scalability and efficiency, safeguarding private user data, and standardising blockchain transactions.
