GANs, a revolutionary machine learning framework, have transformed how computers generate realistic data.
What is a Generative Adversarial Networks (GAN)?
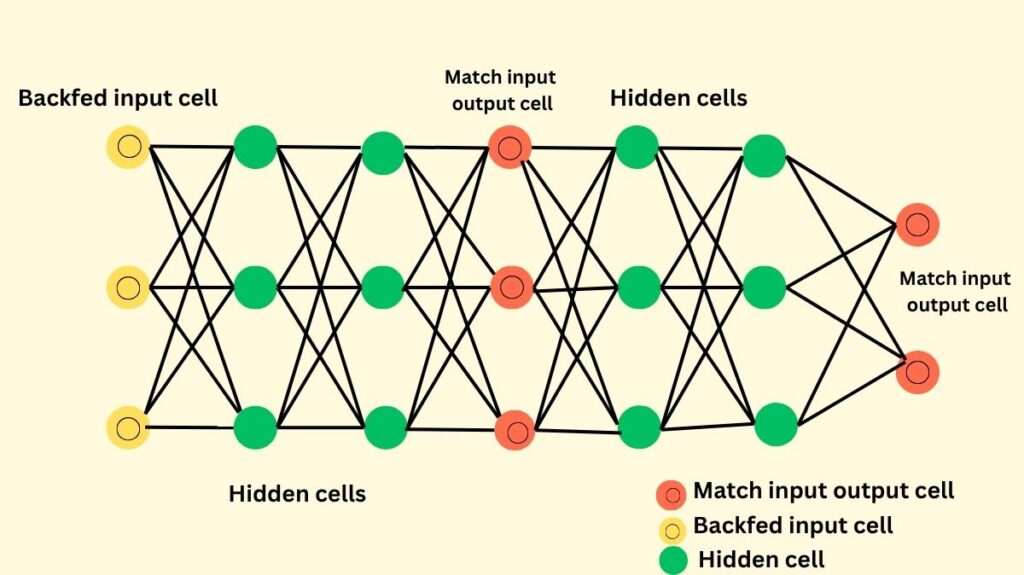
To solve generative modelling, a Generative Adversarial Networks (GAN) was built. In order to create new instances from this estimated distribution, a generative model’s main objective is to analyse a set of training examples and discover the underlying probability distribution that produced them.
With the use of deep learning algorithms and an unsupervised learning framework, generative adversarial networks compete against one another in a cooperative zero-sum game. In other words, the success of one network is the failure of another.
A GAN’s two essential parts are:
- Generator model: The Generator model teaches the network to provide believable facts.
- Discriminator model: This network gains the ability to differentiate between the real data from the training set and the bogus data generated by the generator.
History of GANs
In 2014, Ian Goodfellow and his colleagues presented the idea of Generative Adversarial Networks. Since then, this ground-breaking framework has revolutionized generative modelling by simplifying the process of generating models and algorithms that can produce realistic, high-quality data.
Similar concepts involving adversarial networks were investigated before Goodfellow’s work. Juergen Schmidhuber, for example, wrote a paper on “artificial curiosity” in 1991 that involved neural networks playing a zero-sum game. In 2010, Olli Niemitalo wrote a blog post about a technique that is now called a Conditional generative adversarial networks, or cGAN, for training neural networks to produce missing data in a changeable context. Another source of inspiration was Noise-Contrastive Estimation (NCE), which uses the same loss function as GANs.
How GAN Works
The Generator and Discriminator, two deep neural networks that make up a generative adversarial networks system, train against one other in an adversarial manner.
Generator’s First Move
The generator begins by receiving as input a random noise vector, such as random numbers. It then turns this noise into a fictitious data sample like a produced image by using its internal layers to try to mimic genuine data.
Discriminator’s Turn
The discriminator is given two kinds of information:
- Actual samples taken from the training data.
- The generator produced fake samples. It is the discriminator’s responsibility to examine each input and identify if it is authentic or fraudulent. Usually ranging from 0 to 1, it produces a probability score; a score of 1 denotes that the data is probably authentic, while a score of 0 indicates that it is not.
Also Read About What is Recurrent Neural Networks? and Applications of RNNs
Adversarial Learning
The fundamental mechanism by which generative adversarial networks get better is called adversarial learning.
- The discriminator improves its performance and refines its settings if it accurately classifies both real and bogus data.
- The generator receives a positive update and the discriminator is penalised for its poor decision if the generator is successful in tricking the discriminator by producing realistic fake data.
Generator’s Improvement
The generator gains knowledge from each “success” when the discriminator misinterprets fictitious data for authentic data. The generator consistently enhances its capacity to produce increasingly realistic and believable fake samples across numerous iterations.
Discriminator’s Adaptation
At the same time, the discriminator keeps learning and improving to identify phoney data.
Training Progression
Over time, both networks get stronger because to this never-ending “cat-and-mouse” game. The generator gets increasingly good at creating realistic data as training goes on. When the discriminator eventually finds it difficult to tell the difference between real and fake, the generative adversarial networks is said to be well-trained. The generator can now generate high-quality synthetic data for a range of uses. Backpropagation is used to optimize both networks, calculating the gradient of the loss function and adjusting parameters to minimise the loss.
Advantages and disadvantages of gan
Advantages of GANs
generative adversarial networks are effective artificial intelligence tools because they provide a number of noteworthy advantages.
Synthetic Data Generation
Generating fresh, synthetic data that closely mimics actual data distributions is possible using generative adversarial networks. This is very helpful for creative activities, anomaly detection, and data augmentation (adding training sets for machine learning models).
High-Quality Results
They can create lifelike photos, films, audio, and other material.
Unsupervised Learning
GANs can be used in circumstances where labelling is expensive or difficult to get because they do not require labelled data for training.
Versatility
Generative adversarial networks are versatile for anomaly detection, style transfer, picture synthesis, and text-to-image generation.
Sharp Distributions
In contrast to certain Markov chain-based techniques that need hazy distributions for mixing, they are able to depict extremely clear, even degenerate, distributions.
Computational Efficiency
Because generative adversarial networks only use backpropagation for gradients and do not require Markov chains for training or sampling, they have computational advantages. In comparison to some other models, such as transformers, they can provide faster inference times and frequently have a lightweight architecture.
Disadvantages of GANs
Despite its potential, generative adversarial networks have a number of disadvantages.
- Training Instability: Unstable convergence is one of the main problems, where the discriminator and generator may not converge correctly or improve gradually, producing outputs of low quality.
- Mode Collapse: A common problem with GANs is mode collapse, in which the generator continuously generates a small range of outputs without fully capturing the diversity or “modes” of the input data. For instance, a GAN that has been trained on numbers might only produce the number ‘0’.
- Vanishing Gradient: When the discriminator learns too fast and gets too competent, the generator’s gradients become almost zero, inhibiting efficient learning.
- GAN training needs a lot of data and computational power, which may limit its utility.
- Since conventional metrics don’t capture the intricacies and realism of generative adversarial networks-generated data, evaluating their quality may be tricky.
- The generator’s probability distribution is not explicitly displayed, which may complicate analysis.
- Synchronisation: During training, the discriminator and generator must be in perfect sync. If the generator is trained excessively without updating the discriminator, issues such as the “Helvetica scenario” (a type of mode collapse) may arise.
- Ethical Concerns: There are serious ethical questions around the potential malevolent use of GANs because to their capacity to produce incredibly lifelike false content, such as deepfakes (fake photos and movies).
Also Read About Role of Machine Learning in IoT Applications To Industries
Features of GANs
The following are important features of GANs:
- Two Competing Networks: The basic architecture consists of a discriminator neural network and a generator neural network operating against each other.
- Adversarial Process: To promote reciprocal progress, the networks are trained in a zero-sum, adversarial game environment.
- Implicit Generative Models: GANs do not explicitly model the probability function of the data; instead, they are implicit generative models.
- Single-Pass Sample Generation: GANs can produce a whole sample in a single network pass, in contrast to certain autoregressive models.
- Flexible Network Design: The network can theoretically use any differentiable function, making them universal approximators, and there are no restrictions on the kind of function that can be used.
- Backpropagation Training: The backpropagation algorithm is an efficient way to train the entire system.
Types of GANs
GANs come in a wide variety of forms, each intended to solve certain problems or serve a particular function:
Vanilla GAN
This is the most basic and basic kind of GAN. With multi-layer perceptrons (MLPs), the discriminator and generator are usually constructed. Despite being fundamental, they may encounter issues such as unstable training and mode collapse.
Conditional GAN (CGAN)
To direct the generation process, CGANs provide an extra conditional parameter (such as class labels or attributes). By putting the condition into both the generator and discriminator, the model is able to generate particular output categories instead of merely random data.
Deep Convolutional GAN (DCGAN)
Rather than using straightforward MLPs, this version uses Convolutional Neural Networks (CNNs) for both the discriminator and generator. Because DCGANs can produce realistic, high-quality images, they are quite popular for image production. They employ convolutional layers in the discriminator to extract features and transposed convolutions in the generator to upscale.
Laplacian Pyramid GAN (LAPGAN)
Multi-resolution Laplacian Pyramid GAN (LAPGAN) for high-quality photos. Multiple generator-discriminator pairs at different Laplacian pyramid levels improve image details and reduce noise.
Super Resolution GAN (SRGAN)
SRGANs sharpen and realisticize low-quality images while reducing upscaling errors such blurriness.
StyleGAN-1, StyleGAN-2, and StyleGAN-3 are the StyleGAN series
These GANs, which were created by Nvidia, are renowned for creating incredibly realistic, high-resolution photos, especially those of people.
- StyleGAN-1 uses “style latent vectors” to regulate different levels of detail by combining Progressive GAN with neural style transfer.
- StyleGAN-2 offers invertible data augmentation to operate with limited data and transforms convolution layer weights to improve image quality.
- Strict lowpass filters and rotational/translational invariance are used by StyleGAN-3 to solve problems like “texture sticking” and produce smoother transformations.
CycleGAN
Without the need for paired training data, this architecture translates images across two domains. To guarantee that the translated image can be mapped back to the original, it can, for example, change pictures of horses to zebras or daytime images to nighttime ones using a cycle consistency loss.
Self-Attention GAN (SAGAN)
By integrating self-attention modules into both the discriminator and generator, the Self-Attention GAN (SAGAN) is a DCGAN version that can create and preserve consistency of details utilizing signals from all feature locations, not just spatially local ones.
Wasserstein GAN (WGAN)
In order to provide more stable convergence and mitigate issues such as mode collapse and vanishing gradients, the Wasserstein GAN (WGAN) modifies the GAN objective function and discriminator’s strategy set.
InfoGAN
Designed to maximise the mutual information between a subset of the latent variables and the generator’s output in order to learn interpretable and disentangled representations.
Bidirectional GAN (BiGAN)
An encoder network that translates information from the image space back to the latent space is added to the regular GAN to create the Bidirectional GAN (BiGAN). Applications in interpretable machine learning and semi-supervised learning are thus made possible.
BigGAN
The BigGAN architecture is a large-scale GAN that produces images with state-of-the-art performance, particularly for high-resolution images of ImageNet classes. To guarantee convergence during training, it employs a variety of engineering techniques.
SinGAN
An innovative GAN that can generate a variety of samples that capture the internal statistics of a single natural image and develop a generative model from it.
DiscoGAN
DiscoGAN, like CycleGAN, uses two generators and two discriminators to ensure cycle consistency while learning cross-domain associations without paired data.
Also Read About Feed Forward Neural Network Definition And Architecture
Applications of Generative Adversarial Networks
Image Synthesis & Generation
High-resolution visuals, photorealistic avatars, and AI-powered artwork and designs are examples of image synthesis and generation.
Image-to-Image Translation
Image-to-image translation converts black-and-white to colour, drawings to realistic, or daytime to midnight images.
Text-to-Image Synthesis
This approach develops visuals from written descriptions and helps AI create information and art.
Data augmentation
Adding artificial data to machine learning models to improve generalizability and resilience, especially when labelled data is sparse.
Super Resolution
Enhances films, satellite photography, and medical images by upscaling low-resolution photos for clarity and detail.
Medical Applications
Medical applications include forensic facial reconstructions, glaucoma detection, and synthetic medical images (MRI, PET, CT, and X-rays) for teaching and research.
Fashion, Art, and Advertising
Making new fashion designs, making art (such as the painting “Edmond de Belamy”), developing models, inpainting photos, and providing photorealistic product renders.
Science
Modelling high energy jet creation, approximation physics simulations, simulating gravitational lensing for dark matter studies, iteratively reconstructing astronomical images, and reconstructing velocity and scalar fields in turbulent flows. Even new compounds that have been experimentally confirmed in mice have been produced using GANs.
Video applications
Video applications include deepfakes, video retargeting (converting video content to different aspect ratios), modelling motion patterns in videos, and forecasting forthcoming video frames.
Facial Attribute Manipulation
Changing some aspects of a face in pictures, like hair colour, expressions, or the appearance of ageing.
Object detection
Increasing the calibre and variety of training data for models that detect objects, hence enhancing their robustness and performance.
3D Model Generation
Creating new items as 3D point clouds and reconstructing 3D models of objects from 2D pictures.
Text and Speech Generation
Creating content for blogs, articles, and product descriptions as well as making realistic speech sounds (text-to-speech).
Other Uses
Reconstructing a person’s face from their voice, mapping styles in cartography, visualising the effects of climate change on particular homes, demonstrating how a person’s appearance may change with age, and even recreating old-school video games like Pac-Man simply by observing them being played.
Also Read About Neural Networks In NLP: Features, Applications & Use Cases
Comparison with other Generative Models
Even though GANs are quite good, there are other generative models, such Variational Autoencoders (VAEs). As variations of the original dataset, VAEs are probabilistic models that identify patterns and generate new data samples. VAEs produce blurrier outputs but are easier to train than GANs, which produce crisper and more realistic outputs but are unstable. Which GAN or VAE is best depends on task factors such output quality, training stability, and interpretable latent representations.
Tags: Generative adversarial networks an overview, Advantages of gans, Advantages of GAN, Disadvantages of gans, Advantages and disadvantages of gan, Disadvantages of gan, Different types of gans, Types of gans, Applications of generative adversarial networks, History of gans
