Algorithm Process in Python
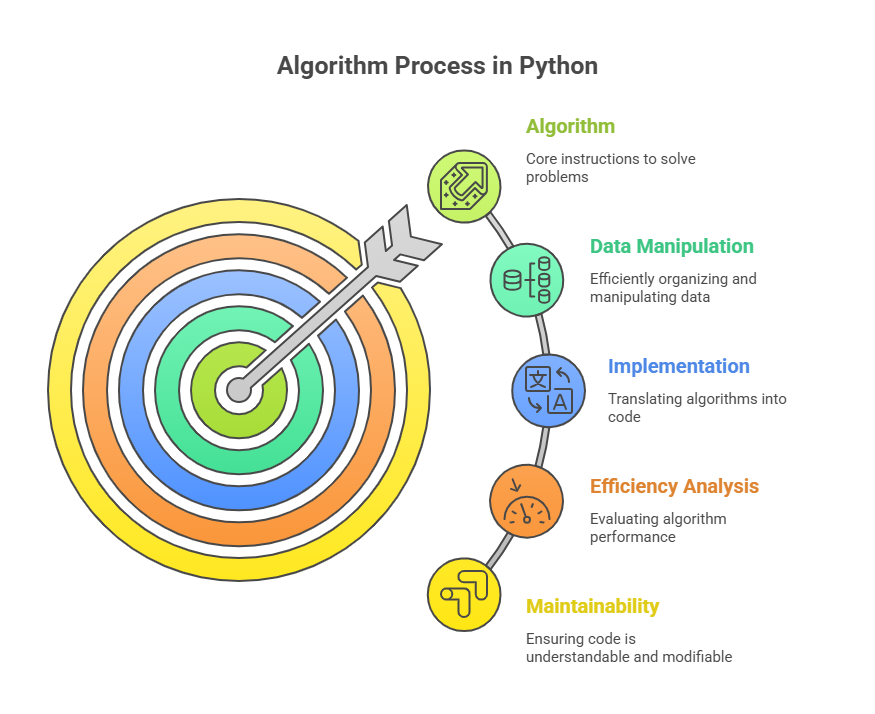
At its core, an algorithm is a collection of instructions designed to solve a problem. More specifically, it is a methodical process for completing a work within a limited time frame. The purpose of these instructions is to efficiently organise and manipulate data.
Anyone who want to understand what computers can accomplish, how they do it, and what they struggle with must have a thorough understanding of algorithms, which are fundamental to computer science.
The Nature of Algorithmic Instructions
Algorithms offer a straightforward, unambiguous method of carrying out a task. Several tools can be used to describe them.
Pseudo-code: A high-level, language-independent description of an algorithm meant for human readers rather than computers is called pseudo-code. It communicates the essential concepts without being mired in minute implementation details by combining programming constructs with conversational language. To make porting to other imperative programming languages easier, many of the algorithms as pseudo-code.
Code Implementation: Python and other programming languages are used to implement algorithms in the end. Because of Python’s popularity and attributes, including its ease of use, object-oriented design, and open-source nature, the book you gave focusses on utilising it to construct data structures and algorithms.
Whatever the description technique, an algorithm usually consists of:
Pre-conditions:Assumptions or prerequisites must be met before an algorithm starts. They are crucial to the algorithm’s operation and should constantly be enforced, especially when adapting algorithms to other programming languages. After the algorithm’s signature, pseudocode lists pre-conditions. A factorial algorithm requires n to be higher than or equal to 0.
Post-conditions:Post-conditions explain a data structure’s intended state following an algorithm. They define what is guaranteed once an algorithm executes. A sorting algorithm post-condition can say “the list has been sorted in ascending order”. Along with pre-conditions, pseudocode lists post-conditions after the algorithm’s signature. If an algorithm’s return type is evident, its post-condition may not include it. Porting algorithms need pre-conditions to avoid uncommon cases.
Base Cases and Recursive Cases: Recursive algorithms describe themselves in terms of themselves, depending on a recursive case that advances towards a base case and one or more base cases to halt the recursion.
The Importance of Algorithms
It is impossible to overestimate the significance of algorithms since they are essential for applying effective code to solve common problems. The following are some main justifications for why knowing algorithms is essential:
Efficiency and Performance: Programs and programmers can work more efficiently with algorithms. What can be calculated with a specific quantity of computing is greatly influenced by the way the data is organised and the algorithms used. Efficiency takes into account both the quantity of memory needed and the time it takes to compute things. Selecting the incorrect method or data structure might cause serious performance problems.
Problem-Solving Capability: Learning conventional algorithms gives you a wealth of information that you can use to solve new issues successfully. This involves being aware of the potential failure points of a specific method or data structure in a given use case.
Selecting the Right Approach: Computer engineers may effectively gather, arrange, and retrieve data by having a thorough understanding of algorithms. It assists in choosing the best algorithms and data structures to satisfy particular programming needs.
Asymptotic Analysis (Big O Notation): Big O notation is one of the mathematical methods used in computer science to accurately analyse and compare algorithms. The performance of an algorithm can be measured abstractly with this notation, enabling evaluation that is not reliant on particular software and hardware configurations. It ignores constant factors and concentrates on the running time growth rate as a function of the input size (n).
Common Growth Rates
- O(1) constant: If a tail pointer is kept, the operation’s time is independent of the size of the input (e.g., adding a node to the tail of a linked list).
- O(log n) logarithmic: Algorithms that regularly split the problem in half, like binary search in a sorted array, frequently use the O(log n) logarithmic method.
- O(n) linear: When searching through an unsorted list, for example, the running time is directly proportional to the size of the input.
- O(n log n): Frequently seen in effective sorting algorithms that divide issues into manageable pieces before combining the outcomes (e.g., merge sort, rapid sort).
- O(n^2) quadratic: Occurs in algorithms that have nested loops, such as bubble sort, when both loops repeat linearly with input size.
- O(n^3) cubic: Extremely uncommon; for larger inputs, this should be avoided.
- O(b^n) exponential: Shows that the method design has to be reviewed; it is not possible for any but the smallest inputs.
Impact of Growth Rates: When the data set gets big enough, an algorithm with a slower growth rate (like logarithmic) will always perform better than one with a higher growth rate (like quadratic), even if the “faster” algorithm has a better constant factor or uses faster hardware.
Maintainability: Program efficiency and maintainability depend on knowing how to arrange elements according to time, function, size, and complexity. The simplicity with which you and other programmers may comprehend and alter your code is known as maintainability.
Identifying a List’s Maximum Element
Example:
def find_max(data):
"""Return the maximum element from a nonempty Python list."""
# Initialize 'biggest' with the first element of the list.
# This is crucial because 'biggest' needs to be a value from the list
# for direct comparison with other elements.
biggest = data
# Iterate through each value in the list.
for val in data:
# If the current value ('val') is greater than the 'biggest' value found so far,
# update 'biggest' to this new larger value.
if val > biggest:
biggest = val
# After checking all elements, 'biggest' will hold the maximum value.
return biggest
# Example 1: Finding the maximum in a list of positive integers
list1 = [10, 4, 20, 5, 15]
max_in_list1 = find_max(list1)
print(f"The maximum element in {list1} is: {max_in_list1}")
# Example 2: Finding the maximum in a list including negative numbers
list2 = [-5, -1, -10, -2, 0]
max_in_list2 = find_max(list2)
print(f"The maximum element in {list2} is: {max_in_list2}")
# Example 3: Finding the maximum in a list with a single element
list3 = [99]
max_in_list3 = find_max(list3)
print(f"The maximum element in {list3} is: {max_in_list3}")
# Example 4: Finding the maximum in a list with floating-point numbers
list4 = [3.14, 1.618, 2.718, 0.5]
max_in_list4 = find_max(list4)
print(f"The maximum element in {list4} is: {max_in_list4}")Output:
The maximum element in [10, 4, 20, 5, 15] is: 20
The maximum element in [-5, -1, -10, -2, 0] is: 0
The maximum element in [99] is: 99
The maximum element in [3.14, 1.618, 2.718, 0.5] is: 3.14Let’s use a straightforward Python code example to demonstrate an algorithm: the find max function, which seeks to determine the maximum entry in a non-empty Python list.
Explanation of the Algorithm as a Set of Instructions
Function Definition (Line 1): The process starts by constructing a function called find max, which accepts the single input argument data, which is assumed to be a non-empty Python list (Line 1). This is the first instruction.
Initialisation (Line 3): The first member of the data list (data) is used to initialise a variable largest. This establishes a starting “candidate” for the highest value. The execution time of this statement is constant.
Iteration (Line 4): The algorithm then moves into a for loop, which iterates through each value in the data list (Line 4). This command starts checking each element one after the other.
Comparison (Line 5): It compares each value with the largest value that is currently in the loop.
Update (Line 6): The algorithm updates biggest to val if val is determined to be greater than biggest. This step guarantees that biggest always contains the highest value that has been found thus far.
Return Value (Line 7): The procedure returns the ultimate biggest value, or the maximum element in the list, once the loop has completed iterating over all of the data’s elements.
Importance and Efficiency of this Algorithm
This find max function is an example of a linear-time algorithm, which means that the number of elements in the data list, or input size n, determines how long the method takes to run. The loop performs a specified number of primitive operations (comparison and possible assignment) on each entry in the list once. As a result, its efficiency is expressed as O(n). Since it already takes n operations to read all n objects into memory, this technique is regarded as efficient for this issue.
