Types of Trees
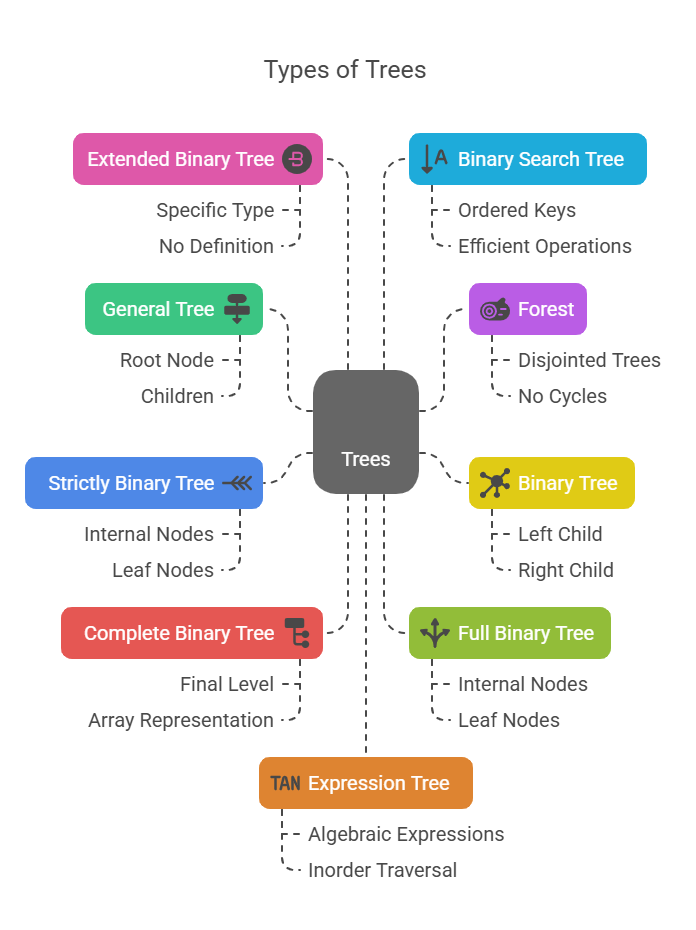
Trees are essential non-linear data structures that allow for hierarchical data organisation in computers and facilitate effective algorithms for a range of tasks. They are frequently found in file systems, databases, and graphical user interfaces and offer benefits over linear data structures like array-based lists or linked lists.
General Tree: An abstract data type known as a “general tree” is one in which all of the elements aside from the root, which is at the top have a parent and zero or more children. Computer applications frequently use nodes to represent entities like files or departments.In an object-oriented programming language, nodes are objects that represent these concepts.
There are no parents for the root, the top node. The parents of every other node are identical. There are two offspring per node in a binary tree, which is different from a generic tree. An example of a linked structure is a generic tree. Additionally, a general tree can be transformed into a binary tree.
Forest: A forest consists of at least one disjointed tree. A graph without any cycles is called a forest. Since a tree is essentially a connected forest that is, a connected graph devoid of cycles this idea fits within the broad category of trees. Trees are seen as a broader class of graphs.
Binary Tree: A binary tree is a specific type of tree in which there can be up to two offspring per node. Because of where they are when they are drawn, these two kids are explicitly referred to as the left and right children. In a binary tree, a node can have no children at all (i.e., it’s a leaf), only left children, or right children. The heights and number of nodes of binary trees are related; level d can have no more than 2^d nodes. It is possible to implement binary trees using an array-based representation or a linked structure.
Strictly Binary Tree: A strictly binary tree is one in which each non-leaf node has precisely two offspring. A strictly binary tree, often called a “proper binary tree” or “full binary tree”. Has nodes with zero or two children. All internal nodes in such a tree will have two children, while leaf nodes will have none. Defines a “full binary tree” as a binary tree with two children for every node except the leaves.
Complete Binary Tree: This type of binary tree has all nodes at the final level as far to the left as feasible and all levels possibly with the exception of the last are fully filled. By numbering the nodes and presuming that all are present to complete the binary tree, an array can be used to represent an incomplete binary tree.
Full Binary Tree: The number of children per node defines a full binary tree. Every node in a full binary tree must have two or zero offspring. This implies that entire binary trees contain two children for every internal nodes. Some call these “proper binary trees”. Half of a balanced full binary tree’s nodes will be on the bottom level, which has one more node than all subsequent levels.
Extended Binary Tree: Listed as a particular kind of binary tree is the Extended Binary Tree. The table of contents lists “Extended Binary Tree” as one of the tree types. In the portions that are provided,Do, not, however, define or explain what a “Extended Binary Tree” is in the sections that are specified.
Binary Search Tree (BST): Node keys are ordered in this binary tree. Right child of a node must have key larger than or equal to parent’s key, whereas left child must have key less. This distinguishes it. This order allows efficient node location, addition, and removal in O(log N) time when the tree is balanced. These operations may become O(N) if an imbalance occurs.
Expression Tree: An algebraic expression can be represented by a binary tree called an expression tree. An expression tree’s inorder traversal, for instance, visits locations in a sequence that corresponds to the expression’s standard form.
Python Building and Operational Procedures
Python may be used to construct and manipulate several of these tree types. The implementation of Binary Search Trees.
Constructing a Binary Search Tree (BST)
Nodes are arranged by their keys in a Binary Search Tree class, which usually starts empty. The constructor sets root node to None. An inner Node class with pointers to the node’s parent, left child, right child, and element is a typical approach to describe tree nodes.
Example:
class BinarySearchTree(object):
"""
A binary search tree class.
The tree organizes nodes by their keys. Initially, it is empty.
"""
def __init__(self):
self.__root = None
# Inner class to represent individual nodes in the tree
class __Node(object):
"""
Non-public class for storing a node.
Each node holds a key and associated data.
"""
def __init__(self, key, data):
self.key = key
self.data = data
self.leftChild = None
self.rightChild = None
def insert(self, key, data):
"""
Inserts a new node with the given key and data into the tree.
If the key already exists, the new node is placed in the right subtree
(allowing for duplicate keys).
"""
newNode = self.__Node(key, data)
if self.__root is None:
self.__root = newNode
return
current = self.__root
while True:
if key < current.key:
if current.leftChild is None:
current.leftChild = newNode
break
current = current.leftChild
else: # If new key is greater than or equal, go right
if current.rightChild is None:
current.rightChild = newNode
break
current = current.rightChild
def search(self, key):
"""
Searches for a node with the given key.
Returns the data associated with the first instance of the key found, None otherwise.
"""
current = self.__root
while current is not None:
if key == current.key:
return current.data
elif key < current.key:
current = current.leftChild
else: # key > current.key or key == current.key (due to insertion logic)
current = current.rightChild
return None
def min_node(self, node=None):
"""
Finds the node with the minimum key in the subtree rooted at 'node'.
If 'node' is None, it starts from the root of the tree.
Returns the node itself.
"""
if node is None:
node = self.__root
if node is None:
return None
current = node
while current.leftChild is not None:
current = current.leftChild
return current
def max_node(self, node=None):
"""
Finds the node with the maximum key in the subtree rooted at 'node'.
If 'node' is None, it starts from the root of the tree.
Returns the node itself.
"""
if node is None:
node = self.__root
if node is None:
return None
current = node
while current.rightChild is not None:
current = current.rightChild
return current
def delete(self, key):
"""
Deletes the node with the given key from the tree.
Note: This implementation will delete the first instance of a key
found during traversal. If duplicate keys exist, only one will be removed.
Returns True if the node was deleted, False otherwise.
"""
# Helper function to find the node and its parent
def _find_node_and_parent(key):
current = self.__root
parent = None
while current is not None:
if key == current.key:
return current, parent
parent = current
if key < current.key:
current = current.leftChild
else: # key > current.key or key == current.key (due to insertion logic for duplicates)
current = current.rightChild
return None, None
node_to_delete, parent = _find_node_and_parent(key)
if node_to_delete is None:
return False
# Case 1: Node to delete is a leaf node
if node_to_delete.leftChild is None and node_to_delete.rightChild is None:
if parent is None:
self.__root = None
elif parent.leftChild == node_to_delete:
parent.leftChild = None
else:
parent.rightChild = None
return True
# Case 2: Node to delete has only one child
if node_to_delete.leftChild is None:
child = node_to_delete.rightChild
if parent is None: # Root node
self.__root = child
elif parent.leftChild == node_to_delete:
parent.leftChild = child
else:
parent.rightChild = child
return True
elif node_to_delete.rightChild is None:
child = node_to_delete.leftChild
if parent is None: # Root node
self.__root = child
elif parent.leftChild == node_to_delete:
parent.leftChild = child
else:
parent.rightChild = child
return True
# Case 3: Node to delete has two children
# Find the in-order successor (smallest in the right subtree)
successor_parent = node_to_delete
successor = node_to_delete.rightChild
while successor.leftChild is not None:
successor_parent = successor
successor = successor.leftChild
# Copy successor's data to the node to be deleted
node_to_delete.key = successor.key
node_to_delete.data = successor.data
# Delete the successor (which now has at most one child)
if successor_parent.leftChild == successor:
successor_parent.leftChild = successor.rightChild
else:
successor_parent.rightChild = successor.rightChild
return True
def inorder_traversal(self):
"""
Performs an in-order traversal of the tree and returns a list
of (key, data) tuples in ascending order of keys.
If duplicate keys exist, they will appear in the order they are visited.
"""
result = []
def _inorder(node):
if node:
_inorder(node.leftChild)
result.append((node.key, node.data))
_inorder(node.rightChild)
_inorder(self.__root)
return result
def is_empty(self):
"""
Checks if the tree is empty.
"""
return self.__root is None
def get_root(self):
"""
Returns the root node of the tree. (For internal/testing purposes)
"""
return self.__root
# Program Usage and Output
if __name__ == "__main__":
bst = BinarySearchTree()
print("--- Inserting elements ---")
bst.insert(50, "Apple")
bst.insert(30, "Banana")
bst.insert(70, "Cherry")
bst.insert(20, "Date")
bst.insert(40, "Elderberry")
bst.insert(60, "Fig")
bst.insert(80, "Grape")
bst.insert(35, "Honeydew")
bst.insert(45, "Ice Cream")
bst.insert(75, "Jalapeno")
bst.insert(85, "Kiwi")
bst.insert(50, "Another Apple")
print("In-order traversal after insertions:")
print(bst.inorder_traversal())
print("-" * 30)
print("\n Searching for elements")
print(f"Search for 40: {bst.search(40)}")
print(f"Search for 90 (not present): {bst.search(90)}")
print(f"Search for 50 (first instance): {bst.search(50)}")
print("-" * 30)
print("\n Min/Max elements ")
min_node = bst.min_node()
if min_node:
print(f"Minimum key: {min_node.key}, Data: {min_node.data}")
else:
print("Tree is empty.")
max_node = bst.max_node()
if max_node:
print(f"Maximum key: {max_node.key}, Data: {max_node.data}")
else:
print("Tree is empty.")
print("-" * 30)
print("\n Deleting elements ")
print("\nDeleting 20 (leaf node):")
bst.delete(20)
print("In-order traversal after deleting 20:")
print(bst.inorder_traversal())
print("\nDeleting 60 (node with one child - right):")
bst.delete(60)
print("In-order traversal after deleting 60:")
print(bst.inorder_traversal())
print("\nDeleting 30 (node with two children):")
bst.delete(30)
print("In-order traversal after deleting 30:")
print(bst.inorder_traversal())
print("\nDeleting 50 (root node with two children):")
bst.delete(50) # This will delete the first 50 encountered
print("In-order traversal after deleting 50:")
print(bst.inorder_traversal())
print("\nAttempting to delete non-existent key (99):")
print(f"Deletion successful: {bst.delete(99)}")
print("In-order traversal (should be unchanged):")
print(bst.inorder_traversal())
print("\n Emptying the tree")
keys_to_delete = [80, 40, 35, 45, 70, 75, 85, 50]
for key in keys_to_delete:
print(f"Deleting {key}...")
bst.delete(key)
print("In-order traversal after emptying:")
print(bst.inorder_traversal())
print(f"Is tree empty? {bst.is_empty()}")
print("-" * 30)
print("\n Testing on an empty tree ")
empty_bst = BinarySearchTree()
print(f"Is empty_bst empty? {empty_bst.is_empty()}")
print(f"Search for 10 in empty_bst: {empty_bst.search(10)}")
print(f"Delete 10 from empty_bst: {empty_bst.delete(10)}")
print("In-order traversal of empty_bst:")
print(empty_bst.inorder_traversal())Output:
Inserting elements
In-order traversal after insertions:
[(20, 'Date'), (30, 'Banana'), (35, 'Honeydew'), (40, 'Elderberry'), (45, 'Ice Cream'), (50, 'Apple'), (50, 'Another Apple'), (60, 'Fig'), (70, 'Cherry'), (75, 'Jalapeno'), (80, 'Grape'), (85, 'Kiwi')]
Searching for elements
Search for 40: Elderberry
Search for 90 (not present): None
Search for 50 (first instance): Apple
Min/Max elements
Minimum key: 20, Data: Date
Maximum key: 85, Data: Kiwi
Deleting elements
Deleting 20 (leaf node):
In-order traversal after deleting 20:
[(30, 'Banana'), (35, 'Honeydew'), (40, 'Elderberry'), (45, 'Ice Cream'), (50, 'Apple'), (50, 'Another Apple'), (60, 'Fig'), (70, 'Cherry'), (75, 'Jalapeno'), (80, 'Grape'), (85, 'Kiwi')]
Deleting 60 (node with one child - right):
In-order traversal after deleting 60:
[(30, 'Banana'), (35, 'Honeydew'), (40, 'Elderberry'), (45, 'Ice Cream'), (50, 'Apple'), (50, 'Another Apple'), (70, 'Cherry'), (75, 'Jalapeno'), (80, 'Grape'), (85, 'Kiwi')]
Deleting 30 (node with two children):
In-order traversal after deleting 30:
[(35, 'Honeydew'), (40, 'Elderberry'), (45, 'Ice Cream'), (50, 'Apple'), (50, 'Another Apple'), (70, 'Cherry'), (75, 'Jalapeno'), (80, 'Grape'), (85, 'Kiwi')]
Deleting 50 (root node with two children):
In-order traversal after deleting 50:
[(35, 'Honeydew'), (40, 'Elderberry'), (45, 'Ice Cream'), (50, 'Another Apple'), (70, 'Cherry'), (75, 'Jalapeno'), (80, 'Grape'), (85, 'Kiwi')]
Attempting to delete non-existent key (99):
Deletion successful: False
In-order traversal (should be unchanged):
[(35, 'Honeydew'), (40, 'Elderberry'), (45, 'Ice Cream'), (50, 'Another Apple'), (70, 'Cherry'), (75, 'Jalapeno'), (80, 'Grape'), (85, 'Kiwi')]
Emptying the tree
Deleting 80...
Deleting 40...
Deleting 35...
Deleting 45...
Deleting 70...
Deleting 75...
Deleting 85...
Deleting 50...
In-order traversal after emptying:
Is tree empty? True
Testing on an empty tree
Is empty_bst empty? True
Search for 10 in empty_bst: None
Delete 10 from empty_bst: False
In-order traversal of empty_bst:Together with pointers to its left and right children, the key and data would be contained in the Node class. For debugging, you can add its str() function to display contents without displaying child nodes.
Building an Expression Tree
It is possible to create an expression tree from a postfix expression. Although whole subtrees are kept on a stack rather than operands, the method is comparable to evaluating a postfix expression. Upon encountering an operand (variable or number), the stack is pushed with the trivial tree that contains that value. A new subtree with the operator as the root is created by combining two subtrees from the stack when an operator is found.
Example:
class ExpressionTree:
"""
Represents a node in an expression tree.
Can be an operator or an operand (literal/variable).
"""
def __init__(self, value, left=None, right=None):
self.value = value
self.leftChild = left
self.rightChild = right
def attach(self, left, right):
"""
Attaches left and right children to this node.
Used when an operator node is created and its operands (subtrees) are identified.
"""
self.leftChild = left
self.rightChild = right
def is_leaf(self):
"""
Checks if this node is a leaf node (i.e., an operand).
"""
return self.leftChild is None and self.rightChild is None
def inorder_expression(self):
"""
Performs an in-order traversal to reconstruct the infix expression.
Adds parentheses to correctly represent operator precedence based on tree structure.
"""
if self.is_leaf():
return str(self.value)
else:
left_expr = self.leftChild.inorder_expression()
right_expr = self.rightChild.inorder_expression()
# For operators, put parentheses around the sub-expression
return f"({left_expr} {self.value} {right_expr})"
# Conceptual steps based on build_expression_tree [73, 74]
def build_expression_tree(tokens):
"""
Builds an expression tree from a list of tokens in postfix (Reverse Polish Notation) order.
Args:
tokens (list): A list of strings representing the postfix expression.
Operators: '+', '-', '*', '/'
Operands: Numbers or variables
Returns:
ExpressionTree: The root node of the constructed expression tree.
"""
S = []
operators = {'+', '-', '*', '/'}
for t in tokens:
if t in operators:
# Pop right and left operands (subtrees)
# Ensure there are enough operands on the stack
if len(S) < 2:
raise ValueError(f"Invalid postfix expression: Not enough operands for operator '{t}'")
right_subtree = S.pop()
left_subtree = S.pop()
# Create a new tree with operator as root and subtrees as children
new_tree = ExpressionTree(t)
new_tree.attach(left_subtree, right_subtree)
S.append(new_tree)
else:
S.append(ExpressionTree(t))
# After processing all tokens, the stack should contain the final expression tree
if len(S) != 1:
raise ValueError("Invalid postfix expression: Stack did not end with a single tree.")
return S.pop()
# Program Usage and Output
if _name_ == "_main_":
print("--- Building Expression Trees ---")
# Example 1: Basic addition
# Postfix: 3 4 + -> Infix: (3 + 4)
tokens1 = ['3', '4', '+']
print(f"\nPostfix Expression: {tokens1}")
try:
tree1 = build_expression_tree(tokens1)
print(f"Infix Expression: {tree1.inorder_expression()}")
except ValueError as e:
print(f"Error: {e}")
# Example 2: Multiplication and addition
# Postfix: 3 4 + 5 * -> Infix: ((3 + 4) * 5)
tokens2 = ['3', '4', '+', '5', '*']
print(f"\nPostfix Expression: {tokens2}")
try:
tree2 = build_expression_tree(tokens2)
print(f"Infix Expression: {tree2.inorder_expression()}")
except ValueError as e:
print(f"Error: {e}")
# Example 3: More complex expression
# Postfix: A B C * + D / -> Infix: ((A + (B * C)) / D)
tokens3 = ['A', 'B', 'C', '*', '+', 'D', '/']
print(f"\nPostfix Expression: {tokens3}")
try:
tree3 = build_expression_tree(tokens3)
print(f"Infix Expression: {tree3.inorder_expression()}")
except ValueError as e:
print(f"Error: {e}")
# Example 4: Expression with subtraction and multiple digits
# Postfix: 10 2 - 3 * -> Infix: ((10 - 2) * 3)
tokens4 = ['10', '2', '-', '3', '*']
print(f"\nPostfix Expression: {tokens4}")
try:
tree4 = build_expression_tree(tokens4)
print(f"Infix Expression: {tree4.inorder_expression()}")
except ValueError as e:
print(f"Error: {e}")
print("\n Testing Error Cases ")
# Error Case 1: Not enough operands
tokens_error1 = ['3', '+']
print(f"\nPostfix Expression (Error Expected): {tokens_error1}")
try:
build_expression_tree(tokens_error1)
except ValueError as e:
print(f"Error caught: {e}")
# Error Case 2: Too many operands/not enough operators
tokens_error2 = ['3', '4', '5', '+']
print(f"\nPostfix Expression (Error Expected): {tokens_error2}")
try:
build_expression_tree(tokens_error2)
except ValueError as e:
print(f"Error caught: {e}")Output:
Building Expression Trees
Postfix Expression: ['3', '4', '+']
Infix Expression: (3 + 4)
Postfix Expression: ['3', '4', '+', '5', '*']
Infix Expression: ((3 + 4) * 5)
Postfix Expression: ['A', 'B', 'C', '*', '+', 'D', '/']
Infix Expression: ((A + (B * C)) / D)
Postfix Expression: ['10', '2', '-', '3', '*']
Infix Expression: ((10 - 2) * 3)
Testing Error Cases
Postfix Expression (Error Expected): ['3', '+']
Error caught: Invalid postfix expression: Not enough operands for operator '+'
Postfix Expression (Error Expected): ['3', '4', '5', '+']
Error caught: Invalid postfix expression: Stack did not end with a single tree.This illustrates how Python implements and uses various tree architectures, striking a balance between academic knowledge and real-world application.